Введение
Для большинства трехмерных приложений работа с камерой состоит из умножения вектора координат положения вершины на матрицы трансформации модели, вида и проекции камеры:
[x', y', z', w'] = [x, y, z, w] * Model * View * ProjectionГде x, y, z — исходные координаты вершины, а x’, y’, z’ — преобразованные к положению камеры. Компонента вектора w называется гомогенной координатой. Для получения трехмерного вектора из гомогенной координаты необходимо разделить компоненты x, y, z координаты на неё. Когда гомогенная координата w равна 0 — вектор считается вектором направления, в остальных случаях получается точка, которую можно сдвинуть.
Пример изменений вершин при умножении на соответствующие матрицы представлен на рисунке 1.
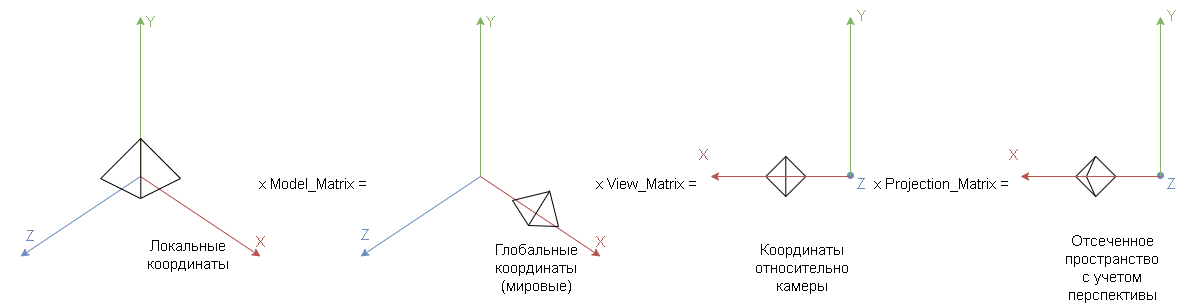
Примечание: матрицу View можно переводить как матрица «вида», но правильнее трактовать её как матрица «местоположения» камеры, а матрица Projection может переводится как «проекции» или «перспективы».
Важное замечание: далее идет много математики между векторами и матрицами, от читателя необходимо понимание: единичных вектора и матрицы; нормирование вектора; сложения, вычитания, скалярного и векторного перемножения векторов; произведения вектора на матрицу.
Матрица трансформации модели
Для перевода из локальных координат модели к глобальным (мировым) координатам используется матрица трансформации, образуемая с помощью трех векторов: перемещения (translate), вращения (rotate), масштабирования (scale).
В библиотеке GLM есть соответствующие функции: glm::translate, glm::rotate, glm::scale. Каждая принимает в качестве первого аргумента матрицу трансформации модели и возвращает измененную версию.
Примечание: матрица трансформации инициализируется единичной матрицей (единицы на главной диагонали).
Функция glm::translate принимает в качестве дополнительного аргумента вектор перемещения модели (dx, dy, dz).
Создается копия исходной матрицы для вычисления результатов. В правый столбец матрицы с результатом записывается вектор образованный из сумм произведений столбцов исходной матрицы трансформации (вектор) на соответствующие составляющие (число) вектора перемещения. Четвертый столбец умножается на 1, так как составляющая не задана. Пример, в котором исходная матрица называется m:
Result[3] = m[0] * dx + m[1] * dy + m[2] * dz + m[3];Функция glm::rotate принимает в качестве дополнительных аргументов значение угла поворота (a) и вектор, определяющий произвольную ось, вокруг которой необходимо произвести поворот модели R(rx, ry, rz).
Рассмотрим простой вариант — повороты вокруг отдельных осей:
| 1 | 0 | 0 | 0 |
| 0 | cos(a) | -sin(a) | 0 |
| 0 | sin(a) | cos(a) | 0 |
| 0 | 0 | 0 | 1 |
| cos(a) | 0 | sin(a) | 0 |
| 0 | 1 | 0 | 0 |
| -sin(a) | 0 | cos(a) | 0 |
| 0 | 0 | 0 | 1 |
| cos(a) | -sin(a) | 0 | 0 |
| sin(a) | cos(a) | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
В ходе вычислений потребуется многократно использовать синус и косинус угла поворота, который необходимо посчитать заранее в отдельные переменные s и c для обеспечения быстродействия.
Создается вспомогательная матрица Rotate, которая состоит из следующих элементов:
| (1-c) * rx2 + c | (1-c) * rx*ry — s*rz | (1-c) * rx*rz + s*ry | 0 |
| (1 — c) * rx*ry + s*rz | (1-c) * ry2 + c | (1-c) * ry*rz — s*rx | 0 |
| (1-c) * rx*rz — s*ry | (1-c) * ry*rz + s*rx | (1-c) * rz2 + c | 0 |
| 0 | 0 | 0 | 1 |
Столбцы матрицы с результатом образуется из суммы столбцов исходной матрицы (вектор), умноженных на ячейки матрицы поворота вокруг произвольной оси [столбец результата][столбец оригинальной] (число).
Пример заполнения матрицы с результатом для исходной матрицы m:
Result[0] = m[0] * Rotate[0][0] + m[1] * Rotate[0][1] + m[2] * Rotate[0][2];
Result[1] = m[0] * Rotate[1][0] + m[1] * Rotate[1][1] + m[2] * Rotate[1][2];
Result[2] = m[0] * Rotate[2][0] + m[1] * Rotate[2][1] + m[2] * Rotate[2][2];
Result[3] = m[3];Функция glm::scale принимает в качестве дополнительного аргумента вектор, определяющий масштабирование по осям (sx, sy, sz).
Создается новая матрица для вычисления результатов. Каждый столбец исходной матрицы (вектор) умножается на соответствующие составляющие (число) вектора масштабирования. Четвертый столбец умножается на 1, так как составляющая не задана. Пример, в котором исходная матрица называется m:
Result[0] = m[0] * sx;
Result[1] = m[1] * sy;
Result[2] = m[2] * sz;
Result[3] = m[3];Пример трансформации модели:
glm::mat4 model(1.0f); // инициализация единичной матрицей
model = glm::translate(model, glm::vec3(1.0f, 0.0f, 0.0f); // перемещение модели по оси Х на 1.0f
model = glm::rotate(model, glm::radians(20.0f), glm::vec3(1.0f, 1.0f, 0.0f)); // поворот вокруг вектора (1.0f, 1.0f, 0.0f) на 20 градусовМатрица местоположения камеры
Матрица местоположения камеры образуется из трех векторов:
- местонахождение камеры в пространстве (а);
- направление камеры — точка в мировых координатах куда смотрит камера (б);
- вектор, указывающий где верх для камеры (в).
Составные элементы матрицы местоположения камеры представлены в на рисунке 2.
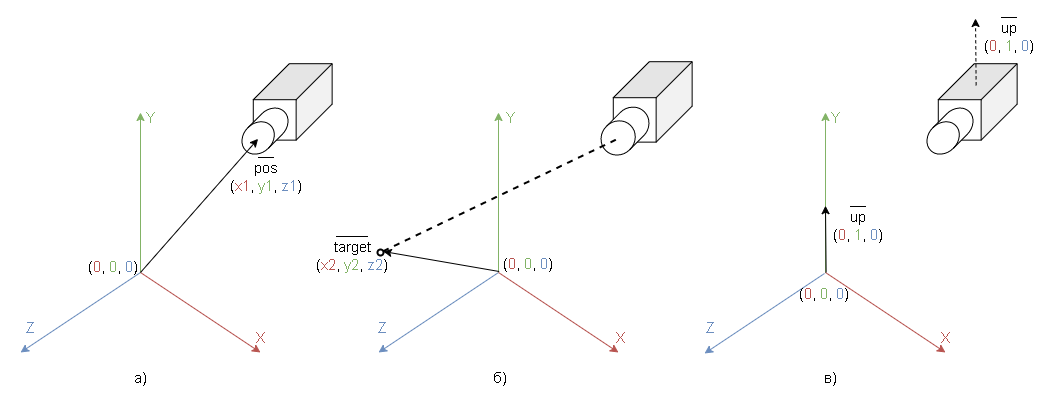
В библиотеке GLM есть функция glm::lookAt, которая возвращает матрицу местоположения камеры и принимает в качестве аргументов три вектора: местонахождение камеры в пространстве (pos), направление камеры (target) и вектор, указывающий где верх для камеры (up).
Рассмотрим алгоритм, лежащий в основе функции glm::lookAt. Для вычисления матрицы местоположения требуется посчитать три вспомогательных вектора:
f = normalize(target - pos)
s = normalize(cross(up, f)) // вектор, определяющий где право для камеры
u = cross(f, s) // вектор, определяющий где верх для камерыФункция normalize возвращает нормированный вектор, который вычисляется делением каждой компоненты на длину вектора. Функция cross возвращает векторное произведение двух векторов.
На рисунке 3 изображены результаты расчетов векторов f, s, u.
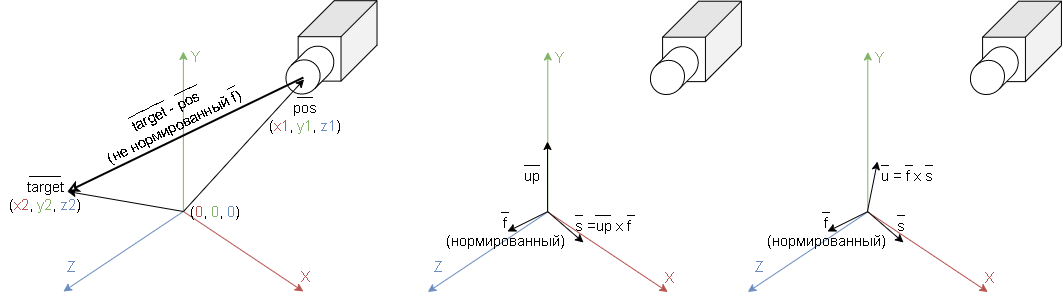
Как можно сделать вывод из рисунка 2: вектор u это нормализованный вектор up. По идее можно было просто вызвать функцию normalize.
На основании посчитанных векторов можно составить следующие матрицы, произведение которых будет матрицей местоположения камеры:
| s.x | s.y | s.z | 0 |
| u.x | u.y | u.z | 0 |
| -f.x | -f.y | -f.z | 0 |
| 0 | 0 | 0 | 1 |
X
| 1 | 0 | 0 | -pos.x |
| 0 | 1 | 0 | -pos.y |
| 0 | 0 | 1 | pos.z |
| 0 | 0 | 0 | 1 |
У правой матрицы вектор позиции камеры инвертирован, так как мировые координаты должны двигаться в противоположном положению камеры.
Так как в правой части произведения находится почти единичная матрица — можно заменить произведение следующим выражением:
| s.x | s.y | s.z | 0 |
| u.x | u.y | u.z | 0 |
| -f.x | -f.y | -f.z | 0 |
| -dot(s, pos) | -dot(u, pos) | dot(f, pos) | 1 |
Функция dot возвращает результат скалярного произведения двух векторов (число).
Пример получения матрицы местоположения камеры с помощью библиотеки GLM:
glm::mat4 view = glm::lookAt( glm::vec3(0.0f, 0.0f, 3.0f)
, glm::vec3(0.0f, 0.0f, 0.0f)
, glm::vec3(0.0f, 1.0f, 0.0f)
);Матрица проекции камеры
Матрица проекции камеры задает пространство усечения, которое задает пространство за рамками которого вершины не рисуются.
В трехмерных приложениях используются два вида матриц проекции:
- ортографическая — пространство представлено параллелограммом;
- перспективная — пространство представлено усеченной пирамидой.
Примеры матриц проекции представлены на рисунке 4. Красный параллелепипед отсекается.
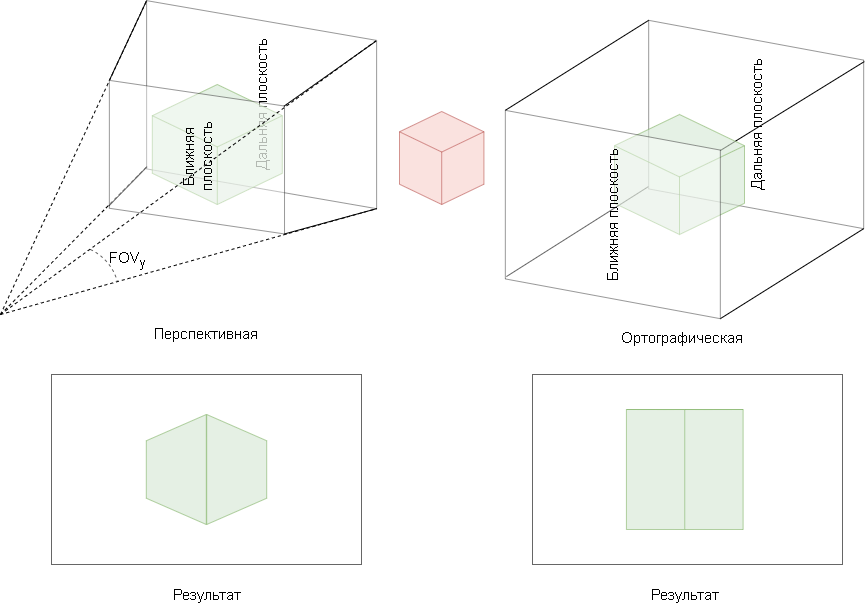
Для создания перспективной матрицы проекции в библиотеке GLM предназначена функция glm::perspective, которая принимает в качестве аргументов угол вертикального обзора(FOVy), отношение сторон экрана (aspect) и пару минимум и максимум для z-буфера (zNear, zFar).
Перспективная матрица проекции создает эффект перспективы: дальние объекты меньше объектов расположенных ближе к камере. Данный эффект достигается путем увеличения w-компоненты (гомогенной координаты) по мере отдаления объекта от камеры.
Способ расчета перспективной матрицы:
| 1 / (aspect * tan(FOVy / 2)) | 0 | 0 | 0 |
| 0 | 1 / tan(FOVy / 2) | 0 | 0 |
| 0 | 0 | — (zFar + zNear) / (zFar — zNear) | -1 |
| 0 | 0 | — (2 * zFar * zNear) / (zFar — zNear) | 0 |
Пример создания перспективной матрицы проекции:
glm::mat4 proj = glm::perspective(45.0f, (float)window_width/(float)window_height, 0.1f, 100.0f);
// FOVy = 45, aspect = width/height, zNear = 0.1, zFar = 100.0Для создания ортографической матрицы проекции в библиотеке GLM предназначена функция glm::ortho, которая принимает в качестве аргументов две пары минимальных и максимальных координат (left, right, bottom, top). Помимо этого есть вариант функции, которая дополнительно принимает пару для z-буфера (zNear, zFar).
Ортографическая матрица считается следующим способом:
| 2 / (right — left) | 0 | 0 | -(right + left) / (right — left) |
| 0 | 2 / (top — bottom) | 0 | -(top + bottom) / (top — bottom) |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 2 / (right — left) | 0 | 0 | -(right + left) / (right — left) |
| 0 | 2 / (top — bottom) | 0 | -(top + bottom) / (top — bottom) |
| 0 | 0 | 1 / (zFar — zNear) | -zNear / (zFar — zNear) |
| 0 | 0 | 0 | 1 |
Пример создания ортографической матрицы проекции, где aspect это отношение ширины к высоте:
glm::ortho(-1.0f, 1.0f, -1.0f/aspect, 1.0f/aspect, 0.1f, 100.0f);Вывод
В рамках данной заметки рассмотрены способ трансформации вершин модели (перемещение, вращение, масштабирование) и устройство камеры (матрица местоположения камеры и проекции).