OpenGL 18: освещение ч.4 — физически-корректный рендеринг

Введение

Современные приложения, работающие с трехмерной графикой, постепенно отходят (по большей части отошли) от модели расчета освещения по Фонгу, на замену которой приходит PBR — физически-корректный рендеринг. Например UE и Unity используют PBR.

Изначально PBR был разработан компанией Disney в 2012 году и позднее адаптирован в Epic games для задач рендера в реальном времени.

Содержание заметки:

• теория:
  • излучаемый свет,
  • отраженный свет:
    • падающий свет,
    • закон косинуса Ламберта,
    • двунаправленная функция отражающей способности;
• переделка старого конвейера;
• расчет освещения по модели PBR;

Важное примечание: для обозначения операций используются символы:

1. векторное произведение \overrightarrow{A} × \overrightarrow{B} = вектор;
2. скалярное произведение \overrightarrow{A} • \overrightarrow{B} = скаляр;
3. покомпонентное произведение (Адамара) \overrightarrow{A} ∘ \overrightarrow{B} = вектор;
4. произведение вектора и скаляра \overrightarrow{A} * b = вектор.

Теория

Физически-корректный рендеринг (PBR, physically-based rendering) — это набор техник визуализации, целью которых является физически достоверная имитация света, но при этом данный метод нельзя назвать физическим методом рендера освещения, так как он является лишь приближением.

Важное замечание: реализация предлагаемая в данной заметке направлена на приложения, работающие с компьютерной графикой в реальном времени и требующие малое время на формирование кадра.

Для того, чтобы модель освещения можно было назвать физически-корректной, она должна учитывать:

1. сохранение энергии — энергия отраженного света не превышает энергии падающего;
2. микрограни шероховатых поверхностей — чем более шероховатая поверхность, тем более рассеян отраженный свет;
3. металлическую и диэлектрическую (неметаллическую) природу материала — разные по природе материалы отражают свет по разному;
4. эффект Френеля — свет отражается и преломляется на границе раздела сред.

Использование физически-корректного рендеринга влечет за собой изменения структуры материалов по сравнению с моделью расчета освещения по Фонгу. Модель физически-корректного рендера использует следующие основные свойства материала:

• base color — базовый цвет материала (R, G, B), иногда называется альбедо (albedo), по аналогии с Фонгом — диффузный цвет;
• roughness — шероховатость поверхности [0;1], где 0 — абсолютно гладкая зеркальная поверхность, а 1 — шероховатая матовая поверхность;
• metallic — металличность поверхности, которая определяет металлический блеск [0;1], где 0 — диэлектрическая поверхность (пластик, стекло, резина), а 1 — металл;
• specular — интенсивность блика и отражений [0;1] для диэлектриков.

Для возможности работать с инструментами и отладочными лампочками к материалу будет добавлен дополнительный параметр:

• emitted — цвет излучаемого света материалом (R, G, B).

В большинстве движков доступна возможность загружать текстуры заместо доступных векторных и скалярных значений, что позволяет сократить число материалов, применяемых к разным участкам одной модели.

Важное замечание: свойство металличности добавляет поверхности зеркальный блеск благодаря уменьшению диффузного отражения, что обсуждается далее по теме сохранения энергии, а свойство интенсивности блика влияет на величину зеркальной составляющей диэлектриков.

Рассмотрим взаимосвязь пар параметров на примере окна предпросмотра материала в Blender. На последующих рисунках можно заметить отражения, которые можно создавать с помощью трассировки лучей или карт отражений, но это будет темой отдельной заметки.

На рисунках 1-5 отображена взаимосвязь параметров шероховатости и металличности материалов с шагом 0.2 при интенсивности блика 0.3. На мобильных устройствах рекомендуется открывать изображения в новых вкладках.

Важное замечание: для металлического шарика важно учитывать что вклад в цвет делает отражение черного окружения сцены.

На рисунках 6-10 отображена взаимосвязь параметров блика и металличности материалов с шагом 0.2 при шероховатости 0.3. На мобильных устройствах рекомендуется открывать изображения в новых вкладках.

Примечание: далее следуют математические формулы с обозначениями свойственными теории PBR, которые отличаются от ранее используемых в теории освещения по Фонгу, но автор постарается дать определение всем используемым обозначениям.

Рассмотрим формулы, описывающие поведение материала. Далее свет и цвета будут определяться векторами в цветовом пространстве (RGB). Общая формула освещенности фрагмента имеет следующий вид:
\overrightarrow{L}_o(\overrightarrow{p}, \overrightarrow{ω_0}) = \overrightarrow{L}_e(\overrightarrow{p}, \overrightarrow{ω_o}) + \overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}),
где \overrightarrow{L}_o — исходящий от поверхности свет (outgoing), \overrightarrow{L}_e — излучаемый поверхностью свет (emitted), \overrightarrow{L}_r — отраженный свет (reflected), \overrightarrow{p} — точка поверхности (вектор xyz, описывающий её положение в пространстве), \overrightarrow{ω_o} — направление исходящего от поверхности света (outgoing).
Данное уравнение описывает количество исходящего света (яркость) из точки на поверхности \overrightarrow{p} в выбранном направлении \overrightarrow{ω_o}, которое обычно в реализациях указывает на камеру. Эта яркость является спектральной величиной — состоит из различных компонент света (RGB).

Излучаемый свет

Излучаемый свет \overrightarrow{L}_e — это свет, создаваемый самой поверхностью. Данный вклад света позволяет видеть объекты без источников света (в абсолютной темноте), например они достаточно горячи, чтоб излучать свет в видимом человеческому глазу.

В данной заметке излучаемый свет будет определяться параметром материала emitted, который будет записываться в отдельную текстуру G-буфера и будет задавать начальную освещенность модели.

Примечание: поведение аналогично параметру ka в модели Фонга.

Отраженный свет

Отраженный свет \overrightarrow{L}_r — это весь свет, падающий на точку поверхности из любой точки сцены, который, после частичного поглощения, перенаправляется в направлении \overrightarrow{ω_o}. Этот вклад света отвечает за возможность видеть большинство объектов, поскольку они не излучают видимый свет \overrightarrow{L}_e.

Обычно вклад отраженного света описывается полной интегральной формой:
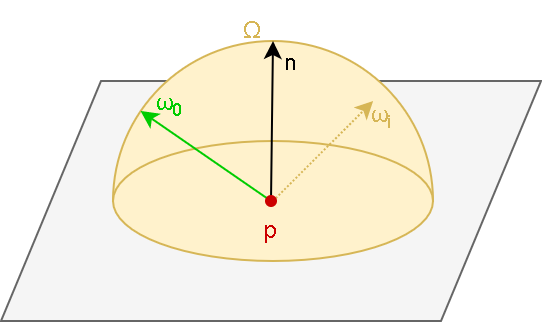
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \int\limits_Ω{\overrightarrow{f}_r(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i})*(\overrightarrow{ω_i} ⋅ \overrightarrow{n})*d\overrightarrow{ω_i}},
где Ω — ориентированная на нормаль \overrightarrow{n} в точке \overrightarrow{p} единичная полусфера, \overrightarrow{f}_r — двунаправленная функция отражающей способности (BRDF), \overrightarrow{L}_i — падающий свет от i источника, а \overrightarrow{ω_i} — направление на i источник. Геометрическое представление данного выражения изображено на рисунке 11.

Рассмотрим три множителя под интегралом:

• \overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i}) — свет, падающий на поверхность от i источника, определяющий максимальная светимость, которая потом ослабляется остальными факторами;
• \overrightarrow{ω_i} ⋅ \overrightarrow{n} — закон косинуса Ламберта, который ослабляет яркость в соответствии с косинусом угла между падающим светом и нормалью поверхности;
• \overrightarrow{f}_r(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}) — двунаправленная функция отражающей способности (BRDF).

Интеграл в данном выражении нужен для того, чтоб учесть все возможные направления (\overrightarrow{ω_i}) падающего света (\overrightarrow{L}_i) для данной точки поверхности (\overrightarrow{p}). На рисунке 12 изображен геометрический смысл данного интеграла. Этот интеграл не может быть решен аналитически для произвольной сцены, вместо этого он может быть либо численно аппроксимирован, либо должны быть сделаны дополнительные предположения для его упрощения.

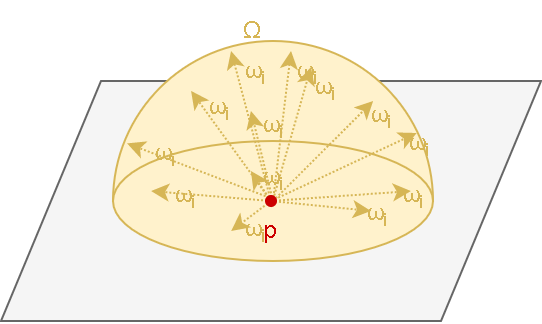
Важное замечание: свет в данной сфере может исходить не только от источников света, но и от других поверхностей (излучаемый и отраженный).

Обычная числовая аппроксимация для автономной визуализации, использующей трассировку лучей, заключается в выполнении выборки методом Монте-Карло по полусфере, после которого требуется выполнить шумоподавление. Если просто, то метод Монте-Карло — метод анализа, применяемый в случаях, когда параметры известны приблизительно, но есть информация о статистическом распределении этих параметров. Для проведения анализа генерируют большое число случайных значений параметров и для каждого значения производят вычисления, которые потом формируют статистическое распределение результата.

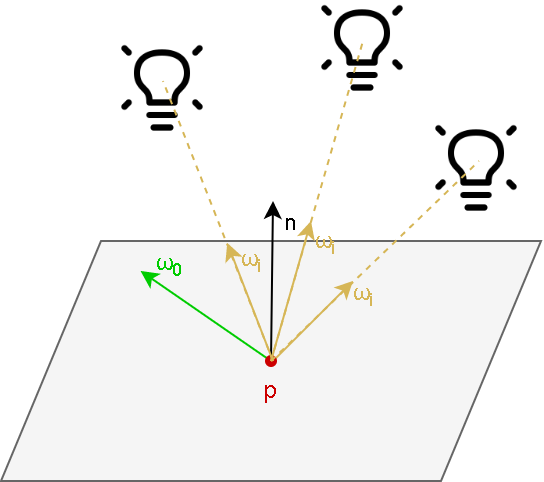
Приложения реального времени обычно делают упрощающее предположение об источниках света, что позволяет решать интеграл аналитически. Предположение заключается в том, что свет, участвующий в отражении от поверхности, могут излучать только источники света, а остальные поверхности на сцене игнорируются. Используя такой подход можно заменить интеграл суммой по источникам света:
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \sum_{i=1}^{N} \overrightarrow{f}_r(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i})*(\overrightarrow{ω_i} ⋅ \overrightarrow{n}),
где N — количество источников света на сцене.
Пример такого упрощения представлен на рисунке 13.

Рассмотрим составляющие отраженного света подробнее.

Падающий свет \overrightarrow{L_i}(\overrightarrow{p},\overrightarrow{ω_i})

Падающий свет определяет количество света от i-ого источника света до точки на поверхности, которое доходит с учетом угасания.

Коэффициент угасания A рассчитывается с помощью трех коэффициентов K_{const}, K_{linear}, K_{quadratic} и дистанции от источника до поверхности d = |\overrightarrow{ω_i}|:
A = K_{const} + K_{linear} * d + K_{quadratic} * d^2

Коэффициенты рассчитываются исходя из радиуса действия источника r:
K_{const} = 1,\\ K_{linear} = 4.5 / r,\\ K_{quadratic} = (2 * K_{linear})^2 = (9 / r)^2

Подробнее о расчете угасания расписано в 9 заметке по расчету освещения.

Итоговый вид падающего света будет иметь следующий вид: \overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i}) = \overrightarrow{color_i} / A = \overrightarrow{color_i} / (K_{const} + K_{linear} * d + K_{quadratic} * d^2),
где \overrightarrow{color_i} — цвет свечения источника.

Важное замечание: для направленного источника (например солнце) не требуется рассчитывать угасание.

Закон косинуса Ламберта \overrightarrow{ω_i} ⋅ \overrightarrow{n}

Скалярное произведение между векторами падения \overrightarrow{ω_i} и нормали поверхности \overrightarrow{n} соответствует значению косинуса угла θ между ними, который ослабляет яркость падающего света в соответствии с законом косинуса Ламберта.

Закон косинуса Ламберта отвечает за затенение поверхностей в зависимости от угла падающих лучей. Этот же закон использовался в модели Фонга.

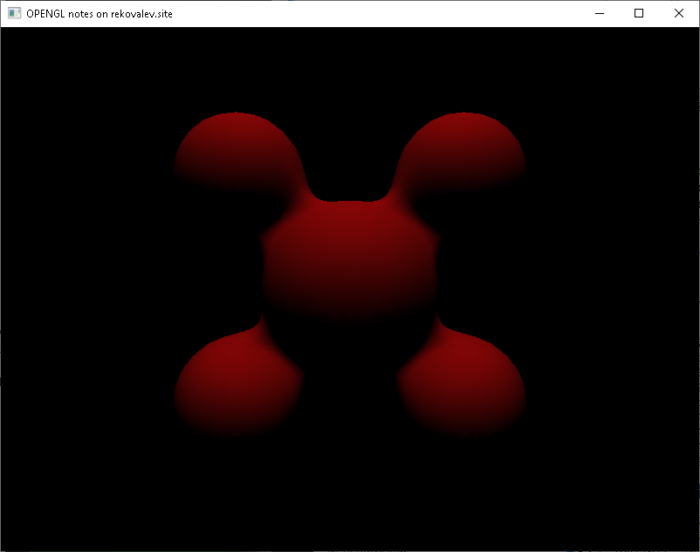
Пример влияния закона косинуса Ламберта на освещенность модели капли от источника, расположенного над ней, изображен на рисунке 14.

Двунаправленная функция отражающей способности \overrightarrow{f}_r(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})

Двунаправленная функция отражающей способности (bidirectional reflectance distribution function, BRDF) — определяет соотношение падающего света в точке поверхности, которое отражается в рассматриваемом направлении \overrightarrow{ω_o} (обычно это вектор на камеру). BRDF моделирует отражательные и преломляющие свойства на основе теории микрограней, для сохранения физической правдоподобности необходимо соблюдение закона сохранения энергии: сумма интенсивностей отраженного света не должна превышать интенсивности приходящего от источника света.

Теория микрограней гласит, что любая поверхность, кажущаяся гладкой в макроскопическом масштабе, в микроскопическом может состоять из большого числа микрограней. Каждая такая микрогрань является оптически плоской, отражая падающий свет в правильном направлении — угол падения равен углу отражения относительно нормали микрограни. Чем более шероховатая поверхность, тем хаотичнее расположены нормали микрограней, делая поверхность материала матовой.

Разберем BRDF:
\overrightarrow{f}_r(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}) = \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}) + \overrightarrow{f}_s(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}),
где \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}) — диффузное отражение, а \overrightarrow{f}_s(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o}) — зеркальное отражение.

Для математического описания закона сохранения энергии допустим что сумма интенсивностей отраженного света в идеальных условиях равна 1:
k_d+k_s=1,
Где k_d — интенсивность диффузного отражения, k_s — интенсивность зеркального отражения. Используя закон сохранения энергии можно упростить вычисления интенсивностей, вычислив лишь одну из них. В реальных условиях эта единица будет уменьшена с помощью угасания с учетом расстояния и косинуса Ламберта (угол падения луча к нормали), а для закона сохранения энергии можно брать 1. Допустим, что k_d = 1 - k_s.

В данной реализации для расчета диффузного отражения будет использоваться формула Ламберта, которая является достаточно простой для вычислений, но при этом менее реалистичной, по сравнению с формулой Орена-Найара.
\overrightarrow{f}_d = k_d * \overrightarrow{f}_{Lambert}, где \overrightarrow{f}_{Lambert} — функция Ламберта:
\overrightarrow{f}_{Lambert} = \frac{\overrightarrow{base\_color_{integral}}}{\pi}.
Далее рассмотрим происхождение числа Пи в данной формуле.

Вернемся к выражению, определяющему отраженный свет, оставив лишь диффузную составляющую (\overrightarrow{f}_r=\overrightarrow{f}_d — в частном случае, а так же \overrightarrow{ω_i} ⋅ \overrightarrow{n} = cosθ):
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \int\limits_Ω{\overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i})*cosθ*dθ}
Данный интеграл можно представить в виде двойного интеграла в полярных координатах:
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \int\limits_{φ=-π}^{π}\int\limits_{θ=0}^{\frac{π}{2}}{\overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i})*cosθ*sinθ*dθdφ},
стоит заметить, что для диффузного отражения \overrightarrow{f}_d — константная величина, которая может быть вынесена за интеграл, а так же для простоты дальнейших вычислений возьмем интенсивность света по полусфере одинаковой:
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i}) \int\limits_{φ=-π}^{π}\int\limits_{θ=0}^{\frac{π}{2}}{cosθ*sinθ*dθdφ}.
Выделим первый интеграл по углу θ:
\int\limits_{θ=0}^{\frac{π}{2}}{cosθ*sinθ*dθ} = \frac{1}{2}\int\limits_{θ=0}^{\frac{π}{2}}{2cosθ*sinθ*dθ} = (*_1),
используя правило произведения для производных:
(f(x)*g(x))' = f'(x)*g(x) + f(x)*g'(x),
выразим (sin^2θ)'=(sinθ*sinθ)' = cosθ*sinθ + sinθ*cosθ = 2cosθ*sinθ,
тогда интеграл упростится до квадрата синуса:
(*_1) = \frac{1}{2}sin^2θ|_{0}^{\frac{π}{2}}=\frac{1}{2}*(sin^2\frac{π}{2} - sin^20) = \frac{1}{2}
Подставив результат во второй интеграл:
\overrightarrow{L}_r(\overrightarrow{p}, \overrightarrow{ω_o}) = \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i(\overrightarrow{p},\overrightarrow{ω_i}) \int\limits_{φ=-π}^{π}{\frac{1}{2}dφ} = \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i * \frac{1}{2} * 2π = \overrightarrow{f}_d(\overrightarrow{p},\overrightarrow{ω_i},\overrightarrow{ω_o})∘\overrightarrow{L}_i * \boldsymbol{π}.
Тут как раз возникает число Пи, которое компенсируется в формуле Ламберта.

Важное замечание: деление на Пи хорошо применимо, когда расчитываются отражения для полусферы, но в упрощении, ведущем к замене интеграла суммой по источникам сцены, деление на Пи в диффузной составляющей не требуется.

Возьмем идеальные условия для диффузного отражения, когда свет абсолютно белый свет (1;1;1) приходит без угасания на абсолютно белую поверхность (1;1;1), представленные в двух вариантах (с делением на Пи и без него) на рисунке 15.

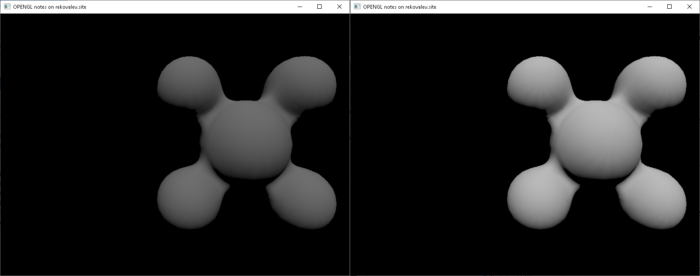
Как можно заметить: левая часть рисунка 15 не является белой, так как деление на Пи не было компенсировано в значениях света или поверхности при замене интеграла суммой по источникам. Обычно в обсуждениях данной проблемы можно встретить простой ответ: «если не хватает света, значит просто прибавьте яркость источника». Автор считает данный подход не корректным и предлагает обозначить, что базовый цвет поверхности для суммы по источникам уже содержит в себе деление на Пи: \overrightarrow{f}_d = \frac{\overrightarrow{base\_color_{integral}}}{\pi} = \overrightarrow{base\_color_{sum}}

Для расчета зеркальной составляющей будет использоваться формула Кука-Торренса (R. Cook и K. Torrance), которая состоит из нормализующего коэффициента в знаменателе и трех функций в числителе:

• D — функция распределения (Distribution function), которая осуществляет аппроксимацию случайного распределения микрограней поверхности, влияющих на шероховатость поверхности;
• F — уравнение Френеля (Fresnel equation), которое описывает соотношение поверхностного отражения при различных углах между поверхностью и падающим светом;
• G — геометрическая функция (Geometry function) — описывает свойство самозатенения на уровне микрограней, что способно снижать общую интенсивность отражаемого света.

Примечание: функция распределения микрограней в статье «Microfacet Models for Refraction through Rough Surfaces» обозначается аббревиатурой GGX.

Данные функции являются аппроксимацией физических эквивалентов с множеством доступных реализаций.

Формула Кука-Торренса для зеркального отражения имеет следующий вид:
\overrightarrow{f}_s = \overrightarrow{f}_{Cook-Torrance}(\overrightarrow{ω_i}, \overrightarrow{ω_o}, \overrightarrow{H}, \overrightarrow{n}, α) = \frac{D\overrightarrow{F}G}{4(\overrightarrow{ω_i} ⋅ \overrightarrow{n})(\overrightarrow{ω_o} ⋅ \overrightarrow{n})},
где \overrightarrow{H} = \frac{\overrightarrow{ω_i} + \overrightarrow{ω_o}}{|\overrightarrow{ω_i} + \overrightarrow{ω_o}|} — вектор половины пути (серединный вектор между векторами на камеру и на источник), который используется в функции распределения согласно UE.

Примечание: можно заметить, что в формуле зеркального отражения отсутствует коэффициент k_s интенсивности зеркального отражения, это связано с тем, что данный коэффициент уже заложен в формулу Кука-Торренса в виде уравнения Френеля. Стоит учитывать, что уравнение Френеля возвращает вектор с коэффициентами для каждого цвета, а в случае коэффициента интенсивности диффузного отражения необходимо рассмотреть проблему искажений с возрастанием металличности:
\overrightarrow{k_d} = 1 - \overrightarrow{k_s} — приводит к искажениям в цветах,
\overrightarrow{k_d} = (1 - \overrightarrow{k_s}) * (1 - metallic) — помимо искажений забирает диффузное отражение сильнее, чем нужно для металлических поверхностей,
k_d = 1 - \frac{|\overrightarrow{k_s}|}{|\overrightarrow{base_{color}}|} — не дает искажений в цветах и позволяет использовать скаляр заместо вектора для диффузного отражения. На рисунке 16 отображено сравнение двух способов для золотой капли с параметрами base_color = (1; 0.86; 0.57), metallic = 0.8, roughness = 0.1, specular = 1.

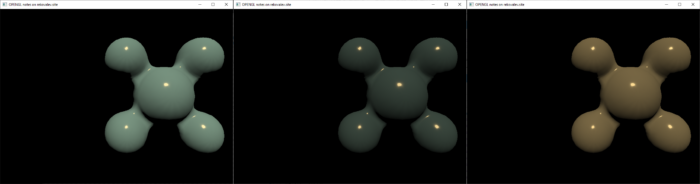
В качестве функции распределения будет использоваться функция нормального распределения (Normalized distribution function, NDF), которая использует вектор половины пути \overrightarrow{H}, нормаль \overrightarrow{n} и коэффициент шероховатости α = roughness^2.

Примечание: параметр материала roughness задается линейно для простоты восприятия шероховатости поверхности, а вычислениях используется его квадрат.

Важное примечание: при описании ориентаций микрограней описывается направление их нормалей к поверхности — неровности создаются нормалями, а не изменением геометрии.

Для функции NDF будет использована модель Троубрижда-Рейца (T. Trowbridge и K. Reitz — авторы модели распределения):
D = NDF_{Trowbridge-Reitz}(\overrightarrow{H},\overrightarrow{n},α) = \frac{α^2}{\pi((\overrightarrow{n} ⋅ \overrightarrow{H})^2(α^2-1)+1)^2}.
В данной функции распределения важно учитывать, что она может возвращать +∞ при малых значениях угла отражения и металличности. Трехмерный график данной функции представлен на рисунке 17.

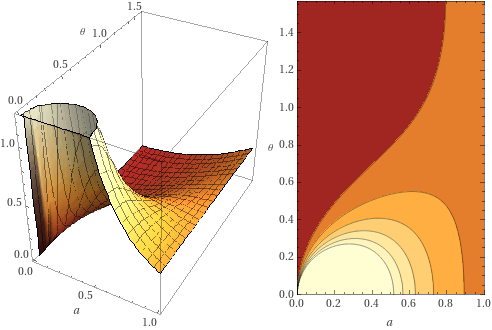
Во избежание нарушения закона сохранения энергии требуется ограничить результат возвращаемый данной функцией до четырех, для нейтрализации влияния четверки в знаменателе функции Кука-Торренса, либо ограничить максимальный результат деленный на четыре единицей.

Для геометрической функции будет использован метод Смита:
G = G_{Smith}(\overrightarrow{ω_i},\overrightarrow{ω_o},\overrightarrow{n},α) = G_{Sclick-Beckmann}(\overrightarrow{ω_i},\overrightarrow{n},α) * G_{Sclick-Beckmann}(\overrightarrow{ω_o},\overrightarrow{n},α),
который в свою очередь использует модель Шлика-Бекмана (C. Schlick и P. Beckmann):
G_{Sclick-Beckmann}(\overrightarrow{ω},\overrightarrow{n},α) = \frac{\overrightarrow{n} ⋅ \overrightarrow{ω}}{(\overrightarrow{n} * \overrightarrow{ω})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}}.
Такой подход позволяет получить более реалистичное изображение.

Стоит заметить, что итоговый вид геометрической функции Смита:
G_{Smith}(\overrightarrow{ω_i},\overrightarrow{ω_o},\overrightarrow{n},α) = \frac{(\overrightarrow{n} ⋅ \overrightarrow{ω_i})}{(\overrightarrow{n} * \overrightarrow{ω_i})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}} * \frac{(\overrightarrow{n} ⋅ \overrightarrow{ω_o})}{(\overrightarrow{n} * \overrightarrow{ω_o})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}}.
В целях упрощения вычислений в этой формуле числитель можно сократить со знаменателем в функции Кука-Торренса,
тогда геометрическая функция примет итоговый вид:
G_{Smith}(\overrightarrow{ω_i},\overrightarrow{ω_o},\overrightarrow{n},α) = \frac{1}{(\overrightarrow{n} * \overrightarrow{ω_i})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}} * \frac{1}{(\overrightarrow{n} * \overrightarrow{ω_o})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}},
а функция Кука-Торренса:
\overrightarrow{f}_{Cook-Torrance}(\overrightarrow{ω_i}, \overrightarrow{ω_o}, \overrightarrow{H}, \overrightarrow{n}, α) = \frac{D}{4}\overrightarrow{F}G

Важное замечание: данная геометрическая функция предназначена для прямого расчета освещения и не подходит для расчета освещения на основе изображения (image-based lighting).

Для расчета освещения на основе изображения используется формула Шлика-Бекмана:
G_{Sclick-Beckmann}(\overrightarrow{ω},\overrightarrow{n},α) = \frac{\overrightarrow{n} ⋅ \overrightarrow{ω}}{(\overrightarrow{n} * \overrightarrow{ω})(1-\frac{(α+1)^2}{2})+\frac{(α+1)^2}{2}}
А так же итоговая форма функции Смита с сокращенным знаменателем:
G_{Smith}(\overrightarrow{ω_i},\overrightarrow{ω_o},\overrightarrow{n},α) = \frac{1}{(\overrightarrow{n} * \overrightarrow{ω_i})(1-\frac{(α+1)^2}{8})+\frac{(α+1)^2}{8}} * \frac{1}{(\overrightarrow{n} * \overrightarrow{ω_o})(1-\frac{(α+1)^2}{2})+\frac{(α+1)^2}{2}}

Уравнение Френеля в оригинальном варианте не подходит для задач рендера трехмерной графики в реальном времени, но можно использовать приближенную модель Френеля-Шлика:
\overrightarrow{F}_{Fresnel-Schlick}(\overrightarrow{H},\overrightarrow{ω_o},\overrightarrow{F}_0,\overrightarrow{F}_{90}) = \overrightarrow{F}_0 + (\overrightarrow{F}_{90} - \overrightarrow{F}_0)(1 - (\overrightarrow{H} ⋅ \overrightarrow{ω_o}))^5,
где \overrightarrow{F_0} — базовая отражательная способность поверхности для лучей параллельных нормали, на которую влияют показатели преломления (indices of refraction, IOR), а \overrightarrow{F}_{90} — зеркальное отражение при углах скольжения (90° между лучом и нормалью).
Для всех материалов принято брать \overrightarrow{F}_{90} = 1, такое поведение поверхности и называется эффектом Френеля. Тогда выражение можно упростить:
\overrightarrow{F}_{Fresnel-Schlick}(\overrightarrow{H},\overrightarrow{ω_o},\overrightarrow{F}_0) = \overrightarrow{F}_0 + (1 - \overrightarrow{F}_0)(1 - (\overrightarrow{H} ⋅ \overrightarrow{ω_o}))^5

В приближении Френеля-Шлика значение базовой отражательной способности для диэлектриков (неметаллических материалов) невероятно мало: (0.0;0.0;0.0) ≤ \overrightarrow{F}_{0\_dielectric} ≤ (0.08;0.08;0.08) для цветовых каналов (RGB). Конкретное значение определяется параметром интенсивности блика диэлектриков, который задается в промежутке [0; 1] и умножается на максимальное значение базовой отражающей способности: \overrightarrow{F}_{0\_dielectric} = (0.08;0.08;0.08) * specular. Для металлов ситуация обстоит сложнее. Рассмотрим разницу отражения света на металлических (проводники) и неметаллических (диэлектрических) поверхностях. Прошу обратить внимание, что речь идет о непрозрачных поверхностях.

К диэлектрикам относятся множество материалов, такие как пластик, камень, дерево, кожа, резина и т.д. Неметаллические поверхности будут отражать зеркальную составляющую света без изменения цвета (цвет блика — соответствует цвету источника), но при преломлении света, некоторые длины волн поглощаются, а остальные излучаются. Данное поведение меняет цвет преломленного света, это изменение света придает этим материалам знакомые цвета (диффузные). Помимо диффузного отраженного света у таких материалов присутствует зеркальная составляющая на которую влияет шероховатость, но так как диффузная составляющая преобладает над зеркальной для таких составляющих.

Идеальные проводники (параметр металличности = 1) с гладкой поверхностью обладают уникальным свойством поглощать весь преломленный свет, так что они не имеют диффузного цвета. При этом они по-прежнему отражают зеркальную составляющую света, изменяя её цвет. То, как металл изменяет этот отраженный свет, определяет цвет, который мы воспринимаем как цвет металла.

Для использования приближения Френеля-Шлика по отношению к металлическим поверхностям необходимо смешать значение базовой отражательной способности для диэлектриков (\overrightarrow{F}_{0\_dielectric}) и базового цвета (\overrightarrow{base\_color}) с учетом параметра металличности. В языке GLSL используется функция mix, которая обеспечивает линейную интерполяцию и принимает три аргумента: \overrightarrow{color_1}— начало диапазона интерполяции, \overrightarrow{color_2} — конец диапазона интерполяции, \overrightarrow{a} — значение (может быть как вектором, так и скаляром), которое используется для интерполяции. Данную функцию можно представить в виде выражения:
mix(\overrightarrow{color_1}, \overrightarrow{color_2}, \overrightarrow{a}) = \overrightarrow{color_1} ⨯ (1 - \overrightarrow{a}) + \overrightarrow{color_2} ⨯ \overrightarrow{a}.
Примечание: если a — скаляр, то можно заменить векторное произведение скалярным.

Переделка старого конвейера

Для начала работы с новыми материалами необходимо изменить структуру материалов и работу с ними, а так же сделать перевод материалов из формата Wavefront в новый.

Важное примечание: можно оставить старые материалы для .OBJ файлов и использовать отдельные шейдеры для них, комбинируя результат с новыми шейдерами.

В файле include/Model.h изменим структуру материала в соответствии с теорией:

// Материал модели
struct Material
{
    alignas(16) glm::vec3 base_color; // Базовый цвет материала
    float roughness; // Шероховатость поверхности
    float metallic; // Металличность поверхности
    float specular; // Интенсивность блика диэлектриков
    alignas(16) glm::vec3 emitted; // Излучаемый поверхностью свет
    int normalmapped; // Использование карт нормалей
    int parallaxmapped; // Использование параллакса
    int displacementmapped; // Использование карт высот для сдвига вершин
    // Значения по умолчанию
    Material() : base_color(0.8f), roughness(0.5f), metallic(0.0f), specular(0.5f), emitted(0.0f), normalmapped(false), parallaxmapped(false), displacementmapped(false) { };
};

По умолчанию материал инициализируется следующими значениями:

• базовый цвет = (0.8;0.8;0.8);
• шероховатость = 0.5;
• металличность = 0.0;
• интенсивность блика = 0.5;
• цвет излучаемого света = (0.0; 0.0; 0.0).

В PBR можно подключить текстуру заместо однородных значений, применяемых ко всей модели. Дополним класс модели текстурами:

class Model : public Node
{
    public:
...
    private:
...
        Texture texture_albedo; // Текстура альбедо (цвет поверхности)
        Texture texture_roughness; // Текстура шероховатостей
        Texture texture_metallic; // Текстура металличности
        Texture texture_emitted; // Текстура излучаемого света
        Texture texture_specular; // Текстура интенсивности блика диэлектриков
        Texture texture_heights; // Текстура высот
        Texture texture_normals; // Текстура нормалей
};

Необходимо исправить конструктор копирования, оператор присваивания, методы Model::render и Model::set_texture в файле src/Model.cpp:

// Конструктор копирования
Model::Model(const Model& copy) : Node(copy),
vao(copy.vao), 
verteces_count(copy.verteces_count), first_index_byteOffset(copy.first_index_byteOffset), indices_count(copy.indices_count), 
vertex_vbo(copy.vertex_vbo), index_vbo(copy.index_vbo), normals_vbo(copy.normals_vbo), texCoords_vbo(copy.texCoords_vbo),
tangent_vbo(copy.tangent_vbo), bitangent_vbo(copy.bitangent_vbo),
texture_albedo(copy.texture_albedo), texture_roughness(copy.texture_roughness), texture_metallic(copy.texture_metallic), texture_specular(copy.texture_specular), texture_emitted(copy.texture_emitted),
texture_heights(copy.texture_heights), texture_normals(copy.texture_normals),
material(copy.material)
...
// Оператор присваивания
Model& Model::operator=(const Model& other)
{
    Node::operator=(other); // Явный вызов родительского оператора копирования
    
    vao = other.vao; 
    verteces_count = other.verteces_count;
    first_index_byteOffset = other.first_index_byteOffset;
    indices_count = other.indices_count;
    
    vertex_vbo = other.vertex_vbo;
    index_vbo = other.index_vbo;
    texCoords_vbo = other.texCoords_vbo;

    tangent_vbo = other.tangent_vbo;
    bitangent_vbo = other.bitangent_vbo;
    
    texture_albedo = other.texture_albedo; 
    texture_roughness = other.texture_roughness; 
    texture_metallic = other.texture_metallic; 
    texture_specular = other.texture_specular; 
    texture_emitted = other.texture_emitted;

    texture_heights = other.texture_heights;
    texture_normals = other.texture_normals;
    
    material = other.material;

    return *this;
}
...
// Вызов отрисовки
void Model::render(ShaderProgram &shaderProgram, UBO &material_buffer) 
{
    // Загрузка идентификатора объекта
    glUniform3uiv(shaderProgram.getUniformLoc("ID"), 1, (GLuint*) &id);

    // Расчитаем матрицу трансформации
    glUniformMatrix4fv(shaderProgram.getUniformLoc("model"), 1, GL_FALSE, &this->getTransformMatrix()[0][0]);

    // Подключаем текстуры
    texture_albedo.use();
    texture_roughness.use();
    texture_metallic.use();
    texture_specular.use();
    texture_emitted.use();
    texture_heights.use();
    texture_normals.use();    

    // Загружаем данные о материале
    material_buffer.load(&material, sizeof(material));

    render();
}
...
// Привязка текстуры к модели
void Model::set_texture(Texture& texture)
{
    GLuint type = texture.getType();
    switch(type)
    {
        case TEX_ALBEDO:
            texture_albedo = texture;
            material.base_color.r = -1;
            break;
        case TEX_ROUGHNESS:
            texture_roughness = texture;
            material.roughness = -1;
            break;
        case TEX_METALLIC:
            texture_metallic = texture;
            material.metallic = -1;
            break;
        case TEX_SPECULAR:
            texture_specular = texture;
            material.specular = -1;
            break;
        case TEX_EMITTED:
            texture_emitted = texture;
            material.emitted.r = -1;
            break;
        case TEX_HEIGHTS:
            texture_heights = texture;
            break;
        case TEX_NORMAL:
            texture_normals = texture;
            break;
    };
}

В файле include/Texture.h необходимо отредактировать перечисление (enum) с типами текстур и заменить значение по умолчанию в конструкторах классов:

...
enum TexType {
    TEX_ALBEDO,
    TEX_ROUGHNESS,
    TEX_METALLIC,
    TEX_SPECULAR,
    TEX_EMITTED,
    TEX_HEIGHTS,
    TEX_NORMAL,
    TEX_AVAILABLE_COUNT
};
...
        Texture(GLuint width, GLuint height, GLuint attachment, GLuint texType = TEX_ALBEDO, GLint internalformat = GL_RGBA, GLint format = GL_RGBA, GLenum dataType = GL_FLOAT); // Конструктор текстуры заданного размера для использования в буфере
        Texture(GLuint width, GLuint height, void* data, GLuint texType = TEX_ALBEDO, GLint internalformat = GL_RGBA, GLint format = GL_RGBA, GLenum dataType = GL_FLOAT); // Конструктор текстуры заданного размера без привязки к буферу с загрузкой пикселей по указателю
...
        TextureArray(GLuint levels, GLuint width, GLuint height, GLuint attachment, GLuint texType = TEX_ALBEDO, GLint internalformat = GL_RGBA, GLint format = GL_RGBA, GLenum dataType = GL_FLOAT); // Конструктор текстуры заданного размера для использования в буфере
...
        TextureCube(GLuint width, GLuint height, GLuint attachment, GLuint texType = TEX_ALBEDO, GLint internalformat = GL_RGBA, GLint format = GL_RGBA, GLenum dataType = GL_FLOAT); // Конструктор текстуры заданного размера для использования в буфере
...
        TextureCube(GLuint width, GLuint height, GLuint attachment, GLuint texType = TEX_ALBEDO, GLint internalformat = GL_RGBA, GLint format = GL_RGBA, GLenum dataType = GL_FLOAT); // Конструктор текстуры заданного размера для использования в буфере
...

Для конвертации параметров будем использовать подход, используемый в Blender 3.5.1:

• базовый цвет (base_color) соответствует диффузному цвету (diffuse или kd);
• шероховатость (roughness) вычисляется как 1 минус корень от дроби — коэффициента зеркального отражения (shininess или Ns), деленного на тысячу;
• металличность (metallic) равна деленной на три сумме компонент фоновой освещенности (ambient или ka);
• интенсивность блика (specular) равна деленной на три сумме компонент зеркальности (specular или ks);
• излучаемый свет (emitted) соответствует излучаемому свету (emission или ke).

В файле src/Scene.cpp в функции загрузки .OBJ файлов loadOBJtoScene сконвертируем материалы в новый формат:

Scene loadOBJtoScene(const char* filename, const char* mtl_directory, const char* texture_directory)
{
...
        // Материал
        s->material.ka = glm::vec3(materials[materials_ids[i]].ambient[0],  materials[materials_ids[i]].ambient[1],  materials[materials_ids[i]].ambient[2]);
        s->material.kd = glm::vec3(materials[materials_ids[i]].diffuse[0],  materials[materials_ids[i]].diffuse[1],  materials[materials_ids[i]].diffuse[2]);
        s->material.ks = glm::vec3(materials[materials_ids[i]].specular[0], materials[materials_ids[i]].specular[1], materials[materials_ids[i]].specular[2]);
        s->material.p  = (materials[materials_ids[i]].shininess > 0.0f) ? 1000.0f / materials[materials_ids[i]].shininess : 1000.0f;
        // Материал
        s->material.base_color = pow(glm::vec3(materials[materials_ids[i]].diffuse[0],  materials[materials_ids[i]].diffuse[1],  materials[materials_ids[i]].diffuse[2]), glm::vec3(1/inv_gamma));
        s->material.roughness = 1 - sqrt(materials[materials_ids[i]].shininess/1000); // шероховатость поверхности
        s->material.metallic = (materials[materials_ids[i]].ambient[0] + materials[materials_ids[i]].ambient[1] + materials[materials_ids[i]].ambient[2]) / 3.0f; 
        s->material.specular = (materials[materials_ids[i]].specular[0] + materials[materials_ids[i]].specular[1] + materials[materials_ids[i]].specular[2]) / 3.0f;
        s->material.emitted = pow(glm::vec3(materials[materials_ids[i]].emission[0],  materials[materials_ids[i]].emission[1],  materials[materials_ids[i]].emission[2]), glm::vec3(1/inv_gamma));
...
}

В методе Фонга текстуры перемножались со значениями параметров материалов, но в PBR используется подход замены параметров на значения из текстуры для конкретного фрагмента с использованием текстурных координат. Можно использовать два подхода для выбора значений между текстурой и параметром материала:

1. в случае, если имеется текстура, используемая заместо параметра — значение параметра устанавливается равным -1, что потом проверяется на шейдере и используется для выбора значения между текстурой и параметром (если параметр < 0, то следует брать значения из соответствующей текстуры);
2. текущая реализация класса текстуры позволяет использовать текстуры-пустышки (1х1 пиксель белого цвета) и в случае, если имеется текстура, используемая заместо параметра — значение параметра устанавливается равным 1, а на шейдере используется перемножение двух параметров;
3. дополнительные флаги к материалам, что увеличивает объем передаваемых данных.

Автор выбирает 1 способ.

Изменим сегмент функции загрузки .OBJ по работе с текстурами: сдвинув сегмент после инициализации параметров и добавив проверки на пустые строки для изменения параметров:

GrouptedModel loadOBJtoGroupted(const char* filename, const char* mtl_directory, const char* texture_directory)
{
...
        // Материал
        s->material.base_color = glm::vec3(materials[materials_ids[i]].diffuse[0],  materials[materials_ids[i]].diffuse[1],  materials[materials_ids[i]].diffuse[2]);
        s->material.roughness = 1 - sqrt(materials[materials_ids[i]].shininess/1000); // шероховатость поверхности
        s->material.metallic = (materials[materials_ids[i]].ambient[0] + materials[materials_ids[i]].ambient[1] + materials[materials_ids[i]].ambient[2]) / 3.0f; 
        s->material.specular = (materials[materials_ids[i]].specular[0] + materials[materials_ids[i]].specular[1] + materials[materials_ids[i]].specular[2]) / 3.0f;
        s->material.emitted = pow(glm::vec3(materials[materials_ids[i]].emission[0],  materials[materials_ids[i]].emission[1],  materials[materials_ids[i]].emission[2]), glm::vec3(1/inv_gamma));
        
        // Текстуры
        if (!materials[materials_ids[i]].diffuse_texname.empty())
        {
            Texture diffuse(TEX_ALBEDO, texture_directory + materials[materials_ids[i]].diffuse_texname);
            s->set_texture(diffuse);
        }
        if (!materials[materials_ids[i]].ambient_texname.empty())
        {
            Texture ambient(TEX_METALLIC, texture_directory + materials[materials_ids[i]].ambient_texname);
            s->set_texture(ambient);
        }
        if (!materials[materials_ids[i]].specular_texname.empty())
        {
            Texture specular(TEX_SPECULAR, texture_directory + materials[materials_ids[i]].specular_texname);
            s->set_texture(specular);
        }
        if (!materials[materials_ids[i]].normal_texname.empty())
        {
            Texture normal(TEX_NORMAL, texture_directory + materials[materials_ids[i]].normal_texname);
            s->set_texture(normal);
        }
        if (!materials[materials_ids[i]].bump_texname.empty())
        {
            Texture heights(TEX_HEIGHTS, texture_directory + materials[materials_ids[i]].bump_texname);
            s->set_texture(heights);
        }

    return result;
}

В файле src/main.cpp удалим принудительное изменение материала для капли, а так же заменим диффузный тип текстур базовым для прямоугольника и скайбокса:

...
    scene.parts[0].material.kd = {0.5,0.5,0.5};
    scene.parts[0].material.ka = {0.05,0.05,0.05};
...
    Texture rectangle_diffuse(TEX_ALBEDO, "../resources/textures/rekovalev_diffusemap.png");
...
    TextureCube skybox_texture(TEX_ALBEDO, {   "../resources/textures/skybox/px.jpg"
                                             , "../resources/textures/skybox/nx.jpg"
                                             , "../resources/textures/skybox/py.jpg"
                                             , "../resources/textures/skybox/ny.jpg"
                                             , "../resources/textures/skybox/pz.jpg"
                                             , "../resources/textures/skybox/nz.jpg"
                                            });
...

И в файле src/Lights.cpp в методе BulbDebug::render заменим фоновую освещенность модели лампочки на базовый цвет в двух местах:

void BulbDebug::render(ShaderProgram &shaderProgram, UBO &material_buffer)
{
...
        bulb_model.parts[0].material.ka = data->color;
        bulb_model.parts[0].material.base_color = data->color;
...
        bulb_model.parts[1].material.ka = data->color;
        bulb_model.parts[1].material.base_color = data->color;
...
}

В заметках используется отложенный рендер, который вычисляет сцену в два прохода: вычисление геометрии (geometry pass) и вычисление освещения (lighting pass). В первом проходе старый формат материалов, который необходимо изменить, запекается в две текстуры, которые затем используются во втором проходе рендера. С новыми материалами они будут иметь следующий формат:

• gBaseColor — базовый цвет, компоненты соответствуют цветам;
• tex_RMS — остальные параметры материала:
  • r = roughness — шероховатость,
  • g = metallic — металличность,
  • b = specular — интенсивность блика.

В файле src/main.cpp изменим название текстур, указав формат GL_RGB:

...
    Texture gBaseColor(WINDOW_WIDTH, WINDOW_HEIGHT, GL_COLOR_ATTACHMENT2, 2, GL_RGB, GL_RGB); // Базовый цвет материала
    Texture gRMS(WINDOW_WIDTH, WINDOW_HEIGHT, GL_COLOR_ATTACHMENT3, 3, GL_RGB, GL_RGB); // Шероховатость, металличность, интенсивность блика
    Texture gID(WINDOW_WIDTH, WINDOW_HEIGHT, GL_COLOR_ATTACHMENT4, 7, GL_RGB32UI, GL_RGB_INTEGER, GL_UNSIGNED_INT); // Идентификатор объекта
    Texture gEmittedColor(WINDOW_WIDTH, WINDOW_HEIGHT, GL_COLOR_ATTACHMENT5, 8, GL_RGB, GL_RGB); // Излучаемый свет
...
        // Подключаем текстуры G-буфера
        gPosition.use();
        gNormal.use();
        gBaseColor.use();
        gRMS.use();
        gID.use();
        gEmittedColor.use();
...

В части указателей для обработки изменений размеров окна буду следующие изменения:

// Указатели на текстуры для изменения размеров окна
Texture* pgPosition = NULL;
Texture* pgNormal = NULL;
Texture* pgBaseColor = NULL;
Texture* pgRMS = NULL;
Texture* pgEmittedColor = NULL;
...
// Функция-callback для изменения размеров буфера кадра в случае изменения размеров поверхности окна
void framebuffer_size_callback(GLFWwindow* window, int width, int height)
{
...
    if (pgBaseColor)
        pgBaseColor->reallocate(width, height, 2, GL_RGB); 
    if (pgRMS)
        pgRMS->reallocate(width, height, 3, GL_RGB, GL_RGB); 
    if (pgEmittedColor)
        pgEmittedColor->reallocate(width, height, 8, GL_RGB, GL_RGB);
...
}
...
int main(void)
{
...
    // Сохраним указатели на текстуры для изменения размеров окна
    pgPosition = &gPosition;
    pgNormal = &gNormal;
    pgBaseColor = &gBaseColor;
    pgRMS = &gRMS;
    pgrbo = &grbo;
    pgID = &gID;
    pgEmittedColor = &gEmittedColor;

Для шейдера, используемого для запекания G-буфера, необходимо изменить имена привязываемых текстур, добавив дополнительную:

...
    const char* textures_base_shader_names[] = {"tex_albedo", "tex_roughness", "tex_metallic", "tex_specular", "tex_emitted", "tex_heights", "tex_normal"};
    gShader.bindTextures(textures_base_shader_names, sizeof(textures_base_shader_names)/sizeof(const char*));
...

Дополнительно требуется изменить имена привязываемых текстур на шейдере lightShader:

...
    const char* gtextures_shader_names[]  = {"gPosition", "gNormal", "gBaseColor", "gRMS", "sunShadowDepth", "pointShadowDepth", "ssao", "gID", "gEmittedColor"};
    lightShader.bindTextures(gtextures_shader_names, sizeof(gtextures_shader_names)/sizeof(const char*));
...

В фрагментном шейдере shaders/gshader.frag запечем материал в текстуры:

layout(std140, binding = 1) uniform Material
{
    vec3 base_color;
    float roughness;
    float metallic;
    float specular;
    vec3 emitted;
    bool normalmapped;
    bool parallaxmapped;
    bool displacementmapped;
};

layout (location = 0) out vec3 gPosition;
layout (location = 1) out vec3 gNormal;
layout (location = 2) out vec3 gBaseColor;
layout (location = 3) out vec3 gRMS;
layout (location = 4) out uvec3 gID;
layout (location = 5) out vec3 gEmittedColor;
...
uniform sampler2D tex_albedo;
uniform sampler2D tex_roughness;
uniform sampler2D tex_metallic;
uniform sampler2D tex_emitted;
uniform sampler2D tex_specular;
uniform sampler2D tex_heights;
uniform sampler2D tex_normal;
...
void main()
{  
...
    // Сохранение базового цвета
    gBaseColor.rgb = base_color.r<0?texture(tex_albedo, new_texCoord).rgb:base_color;
    // Сохранение шероховатости
    gRMS.r = roughness<0?texture(tex_roughness, new_texCoord).r:roughness;
    // Сохранение металличности
    gRMS.g = metallic<0?texture(tex_metallic, new_texCoord).r:metallic;
    // Сохранение интенсивности блика диэлектриков
    gRMS.b = specular<0?texture(tex_specular, new_texCoord).r:specular;
    // Сохранение идентификатора объекта
    gID = ID;
    // Сохранение излучаемого света
    gEmittedColor.rgb = emitted.r<0?texture(tex_emitted, new_texCoord).rgb:emitted;
}

В вершинном шейдере G-буфера shaders/gshader.vert также требуется изменить состав uniform-блока:

layout(std140, binding = 1) uniform Material
{
    vec3 base_color;
    float roughness;
    float metallic;
    float specular;
    vec3 emitted;
    bool normalmapped;
    bool parallaxmapped;
    bool displacementmapped;
};

Для дальнейшей работы над PBR требуется доработать шейдеры инструментов и отладочных лампочек.

В фрагментном шейдере лампочек shaders/bulb.frag в текстуру с излучаемым светом будет записываться базовый цвет лампочки, что позволит не менять текст основной программы:

#version 420 core 

layout(std140, binding = 1) uniform Material
{
    vec3 base_color;
    float roughness;
    float metallic;
    float specular;
    vec3 emitted;
    bool normalmapped;
    bool parallaxmapped;
    bool displacementmapped;
};

...

layout (location = 1) out vec3 gNormal;
layout (location = 3) out vec4 gAmbientSpecular;
layout (location = 4) out uvec3 gID;
layout (location = 5) out vec3 gEmittedColor;
...
void main()
{   
    float cosA = dot(normalize(pos_local), normalize(direction));
    if (degrees(acos(cosA)) <= angle)
        gEmittedColor = pow(base_color, vec3(inv_gamma));
    else
        discard;

...
}

С фрагментным шейдером инструментов shaders/tools.frag требуется проделать аналогичные изменения:

#version 420 core 

layout(std140, binding = 1) uniform Material
{
    vec3 base_color;
    float roughness;
    float metallic;
    float specular;
    vec3 emitted;
    bool normalmapped;
    bool parallaxmapped;
    bool displacementmapped;
};

layout (location = 1) out vec3 gNormal;
layout (location = 3) out vec4 gAmbientSpecular;
layout (location = 4) out uvec3 gID;
layout (location = 5) out vec3 gEmittedColor;

...
void main()
{    
    gNormal = vec3(0);
    // Сохранение базового цвета в качестве излучаемого
    gEmittedColor = base_color;

...
}

Текущая версия отражает некорректное освещение, но все же доступна на теге v0.1 в репозитории 18.

Расчет освещения по модели PBR

Подготовим шейдер shaders/lighting.frag для работы с новыми материалами:

...
uniform sampler2D gPosition;
uniform sampler2D gNormal;
uniform sampler2D gBaseColor;
uniform sampler2D gRMS;
uniform sampler2D gEmittedColor;
uniform sampler2DArray sunShadowDepth;
...
void main() 
{ 
    // Получим данные из текстур буфера
    vec3 fragPos = texture(gPosition, texCoord).rgb;
    vec3 N = texture(gNormal, texCoord).rgb;
    vec3 base_color = texture(gBaseColor, texCoord).rgb;
    float roughness = texture(gRMS, texCoord).r;
    float metallic = texture(gRMS, texCoord).g;
    float specular = texture(gRMS, texCoord).b;
    float ssao_value = texture(ssao, texCoord).r;

Для вычислений по формуле Кука-Торренса необходимо добавить функции, вычисляющие множители из числителя:

const float PI = 3.14159265359;

float D(vec3 H, vec3 N, float a)
{
    float tmp = max(dot(N, H), 0);
    tmp = tmp*tmp*(a*a-1)+1;
    return a*a/(PI * tmp*tmp);
}

float G_Sclick_Beckmann(float NDotDir, float a)
{
    float tmp = (a+1)*(a+1) / 8;
    return 1 / (NDotDir * (1 - tmp) + tmp);
}

float G_Smith(float LDotN, float CamDotN, float a)
{
    return G_Sclick_Beckmann(LDotN, a) * G_Sclick_Beckmann(CamDotN, a);
}

vec3 F(vec3 H, vec3 Cam_vertex, float metallic, vec3 base_color)
{
    vec3 F0 = mix(vec3(0.08 * specular), base_color, metallic);
    return F0 + (1 - F0) * pow(1 - max(dot(H, Cam_vertex),0), 5);
}

Важное замечание: в аргументах функции D (функция распределения) используется переменная a (α) равная квадрату шероховатости (roughness*roughness), вычисляемому в точке вызова.

Реализация работы с тенями останется прежним способом.

Потребуется ввести пять новых переменных, а переменные diffuse и specular более не востребованы и могут быть удалены:

    vec3 Cam_vertex = normalize(camera.position - fragPos); // Расположение камеры относительно фрагмента
    vec3 ks; // Интенсивность зеркального отражения
    vec3 fd, fs; // Диффузное и зеркальное отражения
    float diffuse; // Диффузная составляющая
    vec3 H; // Вектор половины пути
    float specular; // Зеркальная составляющая
...
    float CamDotN; // Скалярное произведение вектора на камеру и нормали
    float LDotN; // Скалярное произведение вектора на источник и нормали

В вычислениях используется скалярное произведение вектора, направленного на камеру, и нормали, которое можно вычислить предварительно и использовать для всех источников света:

    float CamDotN = dot(Cam_vertex,N); // Скалярное произведение вектора на камеру и нормали

Зададим базовую фоновую освещенность сцены на основании значений из текстуры с излучаемым светом:

    // Фоновая освещенность
    color = vec4(texture(gEmittedColor, texCoord).rgb, 1);

Так как у инструментов отсутствует нормаль, то данный шейдер будет рисовать их черными, перезаписывая фоновую освещенность. Во избежание этого добавим проверку, что длинна вектора нормали больше нуля для всех вычислений по источникам света:

    // Если у модели есть нормаль
    if (length(N) > 0)
    {

Рассмотрим вычисление освещенности фрагмента направленным источником (солнце). Базовая часть с вычислением теней имеет следующий вид:

        // Расчет солнца, если его цвет не черный
        if (length(sun.color) > 0)
        {
            // Расположение фрагмента в координатах теневой карты
            fragPosLightSpace = (sun.vp[cascade_index] * vec4(fragPos, 1.0)).xyz;
            // Переход от [-1;1] к [0;1]
            fragPosLightSpace = (fragPosLightSpace + vec3(1.0)) / 2;
            // Сдвиг для решения проблемы акне
            fragPosLightSpace.z -= max(0.05 * (1.0 - dot(N, sun.direction)), 0.005);
            // Проверка PCF
            shadowValue = 0.0;
            texelSize = 1.0 / textureSize(sunShadowDepth, 0).xy; // Размер текселя текстуры теней
            for(x = -1; x <= 1; ++x)
            {
                for(y = -1; y <= 1; ++y)
                {
                    pcfDepth = texture(sunShadowDepth, vec3(fragPosLightSpace.xy + vec2(x, y) * texelSize, cascade_index)).r;
                    shadowValue += fragPosLightSpace.z > pcfDepth  ? 1.0 : 0.0;        
                }    
            }
            shadowValue /= 9.0;
            // Рассчитываем освещенность, если значение тени меньше 1
            if (shadowValue < 1.0)
            {
                // Данные об источнике относительно фрагмента
                L_vertex = normalize(sun.direction);

                // Тут будет вычисление PBR
            }
        }

Так как скалярное произведение вектора, направленного на источник, и нормали используется в вычислениях несколько раз, то вычислим его сразу после вычислений вектора L_vertex и запишем в переменную LDotN:

                // Данные об источнике относительно фрагмента
                L_vertex = normalize(sun.direction);
                LDotN = dot(L_vertex,N);

Примечание: переменная LDotN может быть использована как член произведения, отвечающий за закон косинусов Ламберта в итоговом вычислении освещенности.

Необходимо проверить, что угол между лучом и нормалью положительный:

                if (LDotN > 0)
                {
                    //Дальнейшие вычисления
                }

Вычисление зеркальной составляющей имеет следующий вид:

                    // Вектор половины пути
                    H = normalize(L_vertex + Cam_vertex);

                    // Зеркальное отражение
                    ks = F(H, Cam_vertex, metallic, base_color);
                    fs = ks * min(D(H, N, roughness*roughness) / 4, 1) * G_Smith(LDotN, CamDotN, roughness*roughness);

Результат функции, вычисляющей уравнение Френеля, записывается в отдельную переменную ks, которая будет использована для закона сохранения энергии.

Далее необходимо вычислить диффузное отражение с учетом сохранения энергии и природы материала:

                // Диффузное отражение
                fd = (1 - length(ks)/length(base_color)) * base_color;

Осталось вычислить результирующий свет:

                    // Результирующий цвет с учетом солнца
                    color.rgb += (fd + fs) * sun.color * LDotN * (1.0 - shadowValue);

Примечание: SSAO будет применено к итоговому цвету перед гамма-коррекцией.

Итоговый фрагмент кода шейдера по расчету освещенности направленным источником:

        // Расчет солнца, если его цвет не черный
        if (length(sun.color) > 0)
        {
            // Расположение фрагмента в координатах теневой карты
            fragPosLightSpace = (sun.vp[cascade_index] * vec4(fragPos, 1.0)).xyz;
            // Переход от [-1;1] к [0;1]
            fragPosLightSpace = (fragPosLightSpace + vec3(1.0)) / 2;
            // Сдвиг для решения проблемы акне
            fragPosLightSpace.z -= max(0.05 * (1.0 - dot(N, Sun_direction)), 0.005);
            // Проверка PCF
            shadowValue = 0.0;
            texelSize = 1.0 / textureSize(sunShadowDepth, 0).xy; // Размер текселя текстуры теней
            for(x = -1; x <= 1; ++x)
            {
                for(y = -1; y <= 1; ++y)
                {
                    pcfDepth = texture(sunShadowDepth, vec3(fragPosLightSpace.xy + vec2(x, y) * texelSize, cascade_index)).r;
                    shadowValue += fragPosLightSpace.z > pcfDepth  ? 1.0 : 0.0;        
                }    
            }
            shadowValue /= 9.0;
            // Рассчитываем освещенность, если значение тени меньше 1
            if (shadowValue < 1.0)
            {
                // Данные об источнике относительно фрагмента
                L_vertex = normalize(sun.direction);
                LDotN = dot(L_vertex,N);
                if (LDotN > 0)
                {
                    // Вектор половины пути
                    H = normalize(L_vertex + Cam_vertex);

                    // Зеркальное отражение
                    ks = F(H, Cam_vertex, metallic, base_color);
                    fs = ks * min(D(H, N, roughness*roughness) / 4, 1) * G_Smith(LDotN, CamDotN, roughness*roughness);

                    // Диффузное отражение
                    fd = (1 - length(ks)/length(base_color)) * base_color;

                    // Результирующий цвет с учетом солнца
                    color.rgb += (fd + fs) * sun.color * LDotN * (1.0 - shadowValue);
                }
            }
        }

Применим гамма-коррекцию к итоговому цвету фрагмента:

    // Применение гамма-коррекции
    color.rgb = pow(color.rgb * ssao_value, vec3(inv_gamma));

На рисунке 18 представлен результат вычисления освещенности от солнца с цветом (0.4, 0.4, 0.4) для капли со следующими параметрами материала:

• базовый цвет = (0.5,0.5,0.5);
• шероховатость = 0.3;
• металличность = 0.2;
• зеркальность = 0.5.

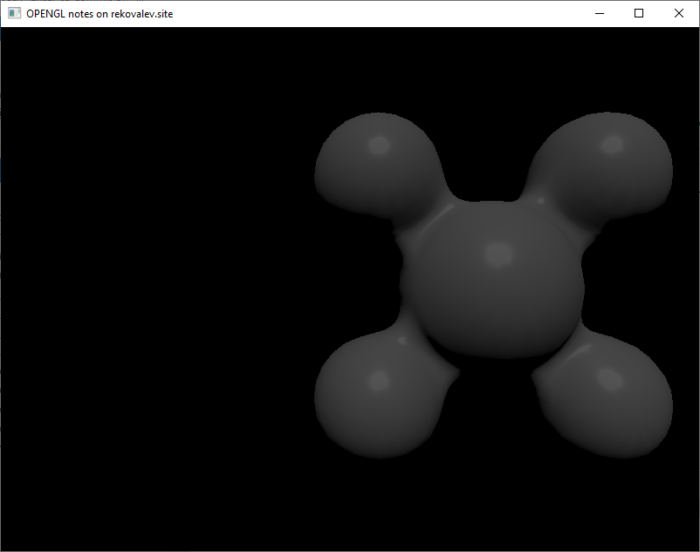
Для точечных источников и прожекторов к итоговому вычислению освещенности добавится учет угасания:

        // Проверка на дистанцию
        if (L_distance < light_f.data[i].attenuation.r)
        {
            // Нормирование вектора
            L_vertex = normalize(L_vertex);
            // арккосинус между вектором от поверхности к источнику и обратным направлением источника
            acosA = degrees(acos(dot(-L_vertex, normalize(light_f.data[i].direction))));
            // Если угол меньше угла источника или угол источника минимален, то считаем освещенность
            if(acosA <= light_f.data[i].direction_angle.a) 
            {
                LDotN = dot(L_vertex,N);
                if (LDotN > 0)
                {
                    // Вектор половины пути
                    H = normalize(L_vertex + Cam_vertex);

                    // Угасание с учетом расстояния
                    attenuation = 1 / (1 + light_f.data[i].attenuation[1] * L_distance + light_f.data[i].attenuation[2] * L_distance * L_distance);

                    // Зеркальное отражение
                    ks = F(H, Cam_vertex, metallic, base_color);
                    fs = ks * min(D(H, N, roughness*roughness) / 4, 1) * G_Smith(LDotN, CamDotN, roughness*roughness);

                    // Диффузное отражение
                    fd = (1 - length(ks)/length(base_color)) * base_color;

                    // Если источник - прожектор, то добавим смягчение
                    if (light_f.data[i].direction_angle.a < 180)
                    {
                        intensity = clamp((light_f.data[i].direction_angle.a - acosA) / 5, 0.0, 1.0);  
                        fd *= intensity;
                        fs *= intensity;
                    }

                    color.rgb += (fd + fs) * light_f.data[i].color * attenuation * LDotN * (1.0 - shadowValue);
                }
            }
        }
    }
}

Результат вычисления освещенности от красного прожектора и синего точечного источника на капле (те же параметры материла) представлен на рисунке 19.

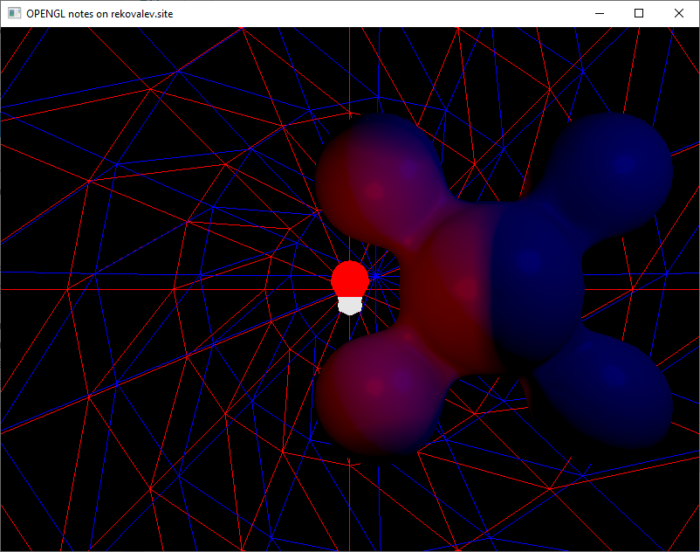
Вернем скайбокс и плоскость на сцену. На рисунке 20 изображен результат вычисления освещенности на старой сцене со скайбоксом.

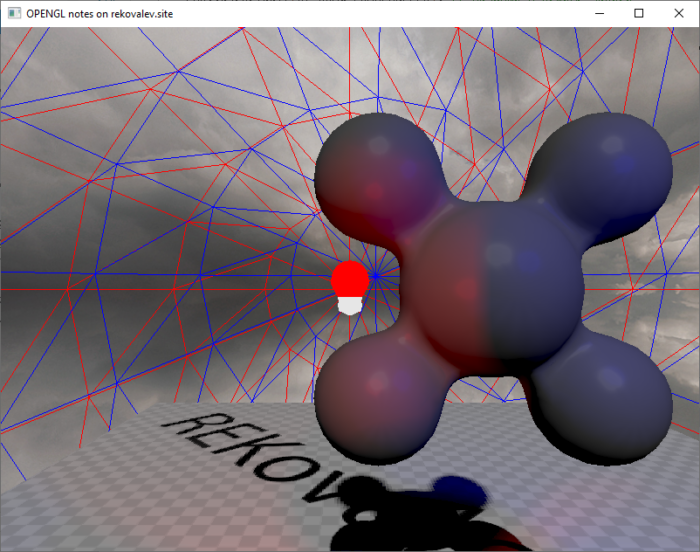
Смотря на последний рисунок можно отметить, что сцена стала темнее, что является следствием соблюдения закона сохранения энергии, которому модель Фонга не соответствовала и порой поверхность отражала больше света, чем на неё попадало. Плюс важно заметить, что все модели теперь по умолчанию имеют нулевую базовую освещенность (излучаемый свет), что так же затемняет картинку.

В дополнение на рисунках 21-23 представлена капля с разными параметрами материалов без скайбокса и цвете солнца (1,1,1).

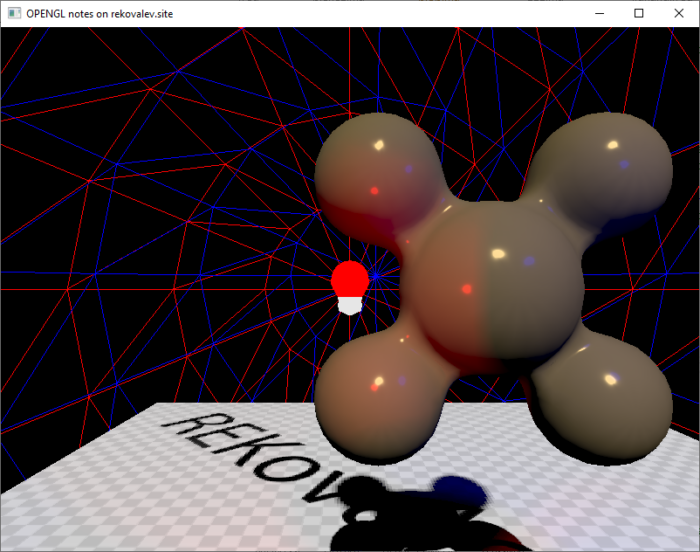
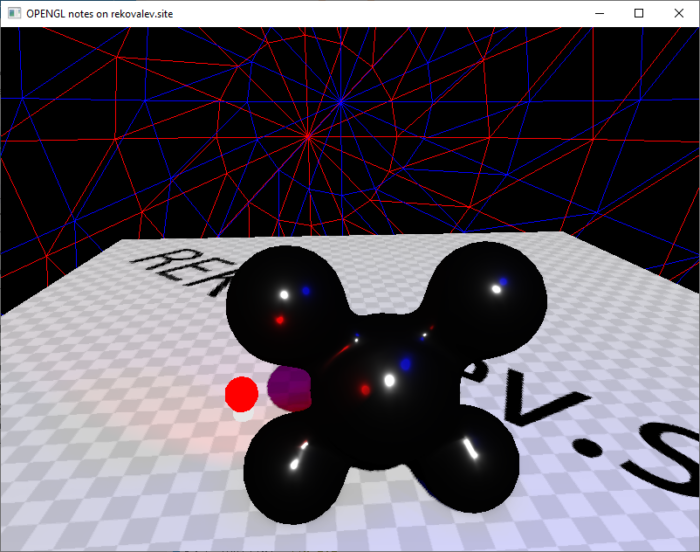
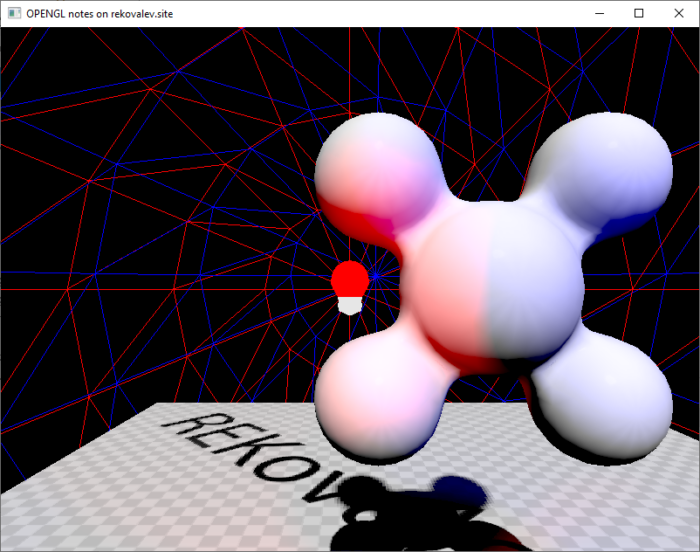
Текущая версия доступна на теге v0.2 в репозитории 18.

Отражения на основании скайбокса

На рисунке 22 можно заметить, что полностью металлическая поверхность становится зеркальной, но при этом черной — ей не хватает зеркальных карт. Тема расчета отражений является достаточно сложной для приложений, работающих в реальном времени и данной теме будет посвящена отдельная заметка. В данной заметке в качестве карты отражения используется текстура скайбокса.

Отражения влияют лишь на зеркальную составляющую, так что диффузная составляющая для зеркальной карты рассчитываться не будет.

Для более шероховатых поверхностей потребуется использовать менее детализированные текстуры для размытия, с чем может помочь генерация Mipmap для текстуры. Перед дальнейшей работой с шейдером необходимо включить генерацию Mipmap и задать фильтрацию с их использованием у кубических текстур в файле src/Textures.cpp:

// Загрузка текстуры с диска или использование "пустой"
TextureCube::TextureCube(GLuint t, const std::string (&filename)[6])
{
...
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); 
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

    glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

    handler_count[handler]++;
}

В файле src/main.cpp ребуется создать копию текстуры скайбокса и задать ей привязку к свободному (9) слоту, так как оригинальная привязывается к 1 слоту для шейдера:

    // Текстура для отражений скайбокса
    TextureCube reflections_texture(skybox_texture);
    reflections_texture.setType(9);

Необходимо инициализировать её значение на шейдере и подключить в процессе рисования:

...
    // Привязка текстур
    const char* gtextures_shader_names[]  = {"gPosition", "gNormal", "gBaseColor", "gRMS", "sunShadowDepth", "pointShadowDepth", "ssao", "gID", "gEmittedColor", "reflections"};
    lightShader.bindTextures(gtextures_shader_names, sizeof(gtextures_shader_names)/sizeof(const char*));
...
        lightShader.use();
        // Очистка буфера цвета и глубины
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        // Подключаем текстуры G-буфера
        gPosition.use();
        gNormal.use();
        gBaseColor.use();
        gRMS.use();
        gID.use();
        gEmittedColor.use();
        reflections_texture.use();
...

Теперь можно добавить uniform-переменную для привязки текстуры в фрагментный шейдер shaders/lighting.frag:

uniform samplerCube reflections;

В разделе теории приведены две версии формулы геометрического распределения, одна из которых используется для расчета освещения на основе изображения — добавим её реализацию к шейдеру освещения:

float G_Sclick_Beckmann_HS(float NDotDir, float a)
{
    float tmp = (a+1)*(a+1) / 2;
    return 1 / (NDotDir * (1 - tmp) + tmp);
}

float G_Smith_HS(float LDotN, float CamDotN, float a)
{
    return G_Sclick_Beckmann_HS(LDotN, a) * G_Sclick_Beckmann_HS(CamDotN, a);
}

Дополнительно потребуется функция Френеля-Шлика с учетом шероховатости для гашения отражений у матовых диэлектриков:

vec3 F_roughness(vec3 H, vec3 Cam_vertex, float metallic, float roughness, float specular, vec3 base_color)
{
    vec3 F0 = mix(vec3(0.08 * specular), base_color, metallic);
    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1 - max(dot(H, Cam_vertex),0), 5);
}

Важное замечание: у инструментов записывается нулевой вектор нормали, что может поломать дальнейшую отрисовку — требуется проверить, что длина вектора нормали больше нуля.

На замену вектору L_vertex придет reflectedVec:

    // Фоновая освещенность
    color = vec4(texture(gEmittedColor, texCoord).rgb, 1);

    if (length(N) > 0)
    {
        // Отражения на основании карт отражений
        vec3 reflectedVec = reflect(-Cam_vertex, N);
...

Так как с возрастанием шероховатости необходимо брать текстуру с уменьшением детализации — будет использоваться функция textureLod, которая помимо привычных параметров принимает третий — уровень mipmap: 0 — оригинальный размер и с возрастанием падает детализация. Пример использования с заданной шероховатостью:

        vec3 reflectedColor = textureLod(reflections, reflectedVec, 8*roughness).rgb;

Вычислим вспомогательные векторы, используемые в дальнейших вычислениях:

        LDotN = dot(reflectedVec, N);

        // Вектор половины пути
        H = normalize(reflectedVec + Cam_vertex);

С их помощью вычислим зеркальную составляющую отражения, использовав её для итогового цвета:

        // Зеркальное отражение
        ks = F_roughness(N, Cam_vertex, metallic, roughness, specular, base_color);
        fs = ks * min(D(H, N, roughness*roughness) / 4, 1) * G_Smith_HS(LDotN, CamDotN, roughness*roughness);

        // Результирующий цвет с учетом солнца
        color.rgb += fs * reflectedColor * LDotN;
    }

Теперь запустим приложение с параметрами материалов капли: base_color = (1; 1; 1), metallic = 0.8, roughness = 0.1, specular = 0.5. Результат работы приложения с заданными параметрами представлен на рисунке 24.

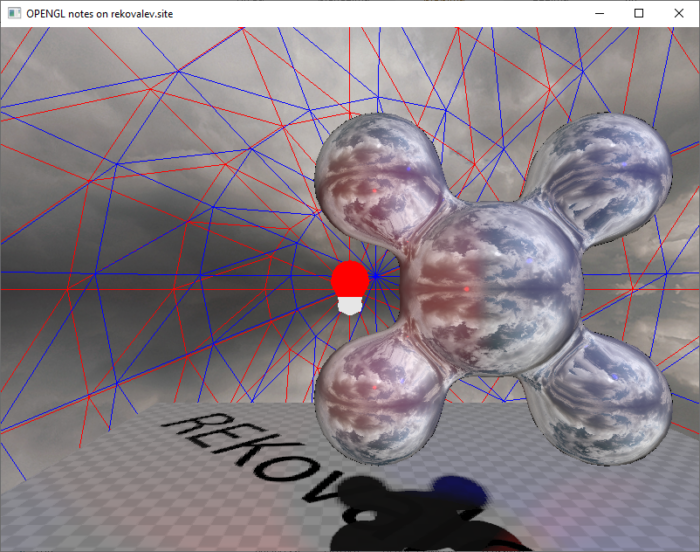
Данную реализацию отражений можно назвать «ленивой», так как она не учитывает другие объекты на сцене и не использует полусферу для расчета освещенности.

Текущая версия доступна на теге v0.3 в репозитории 18.

Заключение

В данной заметке был рассмотрен физически-корректный рендер и материалы, используемые в данном подходе. Был переделан графический конвейер для соответствия новым требованиям, сделана конвертация материалов Wavefront (.OBJ/.MTL) в новый формат в соответствии с Blender, а так же реализован шейдер расчета освещенности, соответствующий правилам PBR.

Проект доступен в публичном репозитории: 18.
Библиотеки: dependencies
Ресурсы: resources