Криптографический алгоритм «Кузнечик» (ГОСТ Р 34.12-2015)

Введение

В целях упрощения информации данная заметка разбита на следующие части:

теоретическая база;
алгоритм «Кузнечик»;
реализация;
тестирование.

Реализацию на языке Си можно найти в репозитории C_Kuznechik_GOST_R_34.12-2015.

Теоретическая база

Для описания работы криптографического алгоритма необходимо рассмотреть поля Галуа из математики, а так же сети Фейстеля из области шифрования.

Поля Галуа

Поле Галуа, так же называемое конечным полем, это поле состоящее из конечного числа элементов. Обозначается как F или GF(q), где q — число элементов поля.

Под термином поля следует понимать множество с двумя бинарными операциями: сложение (аддитивная операция) и умножение (мультипликативная операция), если оно образует коммутативное (a + b = b + a) ассоциативное (a + (b + c) = (a + b) + c) кольцо в котором 1 не равна 0 (то есть нейтральные элементы по сложению и умножению различны).

В свою очередь под термином кольцо следует понимать понимать множество с двумя бинарными операциями: сложение и умножение, со свойствами, напоминающими сложение и умножение целых чисел.

Подробнее с данными терминами и подробной теорией можно ознакомиться в книге Курс алгебры за авторством Винберг Э.Б.

Арифметика полей Галуа — полиномиальная арифметика, то есть каждый элемент данного поля представляет собой некий полином.

Полином из полиномиальной арифметики обычно принято объяснять приводя цитату Д. Кнута из книги Искусство программирования, но определение достаточно сложное и просто вырывать его из контекста книги автор заметки считает некорректным. Вместо этого обозначим «на пальцах», что есть некий многочлен u(x) = u_nxⁿ + … + u₂x² + u₁x¹ + u₀x⁰, который служит для задания чисел, например:

5 = 101 = 1*x² + 0*x¹ + 1*x⁰ = x² + 1 
                              (полиномиальная форма числа 5 для x = 2).

Далее в качестве примера будет использоваться поле Галуа с числом элементов 8 (GF(2³)), которое состоит из чисел от 0 до 7.

В качестве операции сложения в полях Галуа служит побитовое сложение по модулю 2 (XOR). данная операция обозначается плюсом, обведенном в кружок. Пример такого сложения изображен на рисунке 1.

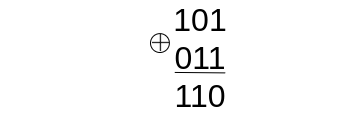
Рисунок 1 — Побитовое сложение по модулю 2

В качестве операции умножения используется умножение полиномиальных форм с применением правил сложения по модулю 2 для слагаемых с одинаковыми степенями. Пример:

7 * 5 = (x² + x + 1) * (x² + 1) = x⁴ + x³ + x² + x² + x + 1 = x⁴ + x³ + x + 1 = 11011 = 27

x2 + x2 = 0, так как сложение по модулю 2

Но результат выходит за пределы ранее заданного поля Галуа. Для решения данной проблемы используется порождающий (неприводимый/простой) полином: x³ + x + 1 равный 0.

С помощью того-же правила сложения по модулю 2 дополним выражение не изменяя результата:

7 * 5 = x⁴ + x³ + x + 1 = (x⁴ + x³ + x + 1) + (x² + x² + x + x) = ...

Далее скомпонуем элементы следующим образом:

... = (x⁴ + x² + x) + (x³ + x + 1) + x² + x = x * (x³ + x + 1) + (x³ + x + 1) + x² + x = ...

Так как порождающий полином = 0, то выражение можно упростить:

... = x² + x = 110 = 6

Вторым вариантом приведения результата умножения к заданному полю Галуа может быть остаток от деления на порождающий полином. Пример деления представлен на рисунке 2.

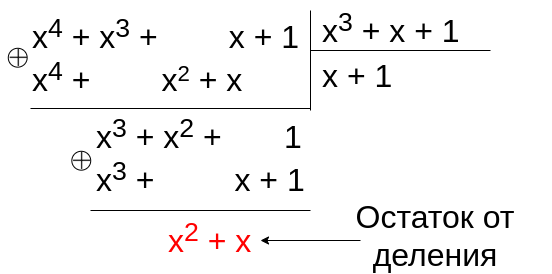
Рисунок 2 — Пример деления для приведения результата умножения к заданному полю Галуа

Примечания к рисунку 2: в процессе расчетов используется сложение по модулю 2, а так же для удобства восприятия между слагаемыми проставлены пробелы если соответствующей степени нет в выражении.

Для простоты можно составить таблицу умножения:

		1	2	3	4	5	6	7
1	1	1	2	3	4	5	6	7
x	2	2	4	5	3	1	7	5
x + 1	3	3	6	5	7	4	1	2
x²	4	4	3	7	6	2	5	1
x² + 1	5	5	1	4	2	7	3	6
x² + x	6	6	7	1	5	3	2	4
x² + x + 1	7	7	5	2	1	6	4	3

Деление можно производить на основании этой таблицы.

Возведение в степень производится аналогично умножению.

числа\степени		0	1	2	3	4	5	6	7
1	1	1	1	1	1	1	1	1	1
x	2	1	2	4	3	6	7	5	1
x + 1	3	1	3	5	4	7	2	6	1
x²	4	1	4	6	5	2	3	7	1
x² + 1	5	1	5	7	6	3	4	2	1
x² + x	6	1	6	2	7	4	5	3	1
x² + x + 1	7	1	7	3	2	5	6	4	1

Примитивный член поля Галуа — элемент поля, чьи степени содержат все ненулевые элементы поля. Для полей с характеристикой 2, в качестве примитивного члена выбирается 2. Например: 6 = 2⁴.

Сеть Фейстеля

Сеть Фейстеля — это метод блочного шифрования, разработанный Х. Фейстелем в лаборатории IBM в 1971 году.

Пример сегмента сети Фейстеля представлен на рисунке 3.

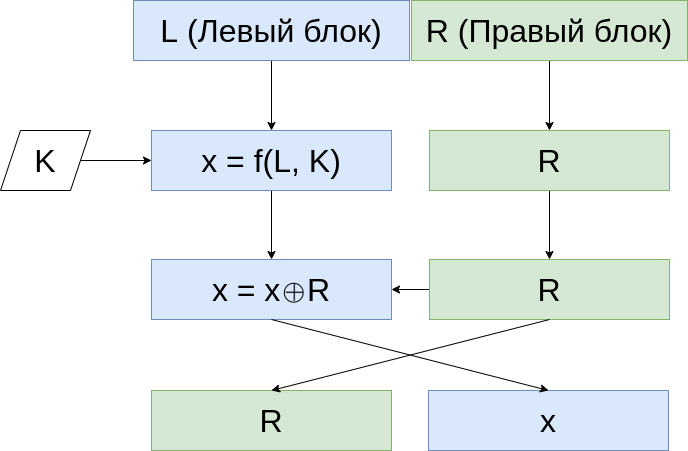
Входной блок сообщения разбивается на два блока (левый и правый). Далее левый блок изменяется функцией f(L, K) с использованием ключа. После этого к левому блоку добавляется правый с помощью побитового сложения по модулю 2 (XOR). Для следующей итерации блоки меняются местами.

Алгоритм «Кузнечик»

Основу алгоритма составляет подстановочно-перестановочная сеть (Substitution-Permutation network — SP сеть), которая является разновидностью сетей Фейстеля.

Шифр на основе SP-сети получает на вход блок и ключ и совершает несколько чередующихся раундов, состоящих из стадий подстановки и стадий перестановки. В «Кузнечике» выполняется девять полных раундов, каждый из которых включает в себя три последовательные операции:

операция наложения итерационного ключа (K_j);
нелинейное преобразование (S);
линейное преобразование (L).

После девяти полных раундов следует последний, состоящий только из операции наложения итерационного ключа (K₁₀) или побитовый XOR ключа и входного блока данных.

Операция наложения итерационного ключа (K_j) — это побитовый XOR ключа и входного блока данных

Нелинейное преобразование (S) представляет собой простую замену одного байта на другой в соответствии с таблицей, представленной в разделе 4.1.1 ГОСТ Р 34.12-2015.

Линейное преобразование (L): каждый байт из блока умножается в поле Галуа на один из коэффициентов ряда (linear_vector): {148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1} в зависимости от порядкового номера байта. Байты складываются между собой по модулю 2, и все 16 байт блока сдвигаются в сторону младшего разряда, а полученное число записывается на место считанного байта.

Общий алгоритм представлен на рисунке 4.

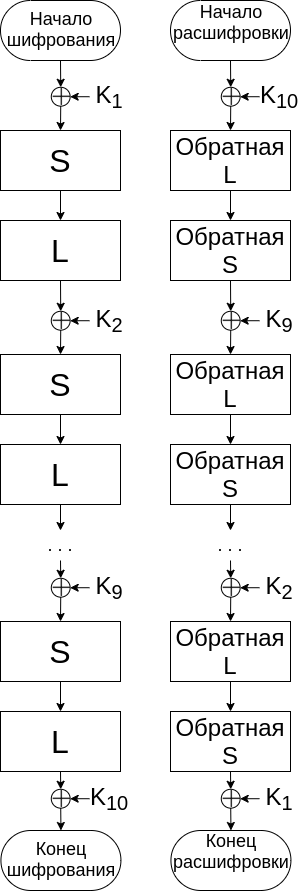
Рисунок 4 — Алгоритм шифрования и расшифровки

Согласно рисунку 4: алгоритм расшифровки производится в обратном порядке с использованием обратных функций L и S.

Итерационные ключи (K_j), они же называются раундовыми, получаются путем преобразований на основе мастер-ключа длинной 256 бит (32 байта). В начале ключ делится на две части, образующие первые два итерационных ключа. Для генерации оставшихся проводится по восемь итераций сети Фейстеля. В каждой итерации используется константа (C_i), которая вычисляется путем применения линейного преобразования алгоритма к значению номера итерации.

Алгоритм генерации ключей представлен на рисунке 5.

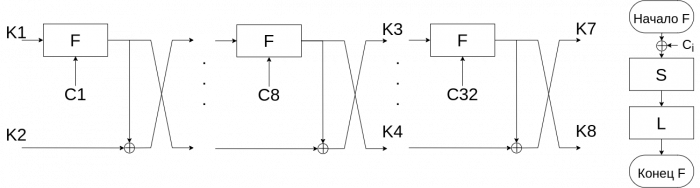
Константы (C_i) для проверки работы последующей реализации:

C01 = 0x6E 0xA2 0x76 0x72 0x6C 0x48 0x7A 0xB8 0x5D 0x27 0xBD 0x10 0xDD 0x84 0x94 0x01 
C02 = 0xDC 0x87 0xEC 0xE4 0xD8 0x90 0xF4 0xB3 0xBA 0x4E 0xB9 0x20 0x79 0xCB 0xEB 0x02 
C03 = 0xB2 0x25 0x9A 0x96 0xB4 0xD8 0x8E 0x0B 0xE7 0x69 0x04 0x30 0xA4 0x4F 0x7F 0x03 
C04 = 0x7B 0xCD 0x1B 0x0B 0x73 0xE3 0x2B 0xA5 0xB7 0x9C 0xB1 0x40 0xF2 0x55 0x15 0x04 
C05 = 0x15 0x6F 0x6D 0x79 0x1F 0xAB 0x51 0x1D 0xEA 0xBB 0x0C 0x50 0x2F 0xD1 0x81 0x05 
C06 = 0xA7 0x4A 0xF7 0xEF 0xAB 0x73 0xDF 0x16 0x0D 0xD2 0x08 0x60 0x8B 0x9E 0xFE 0x06 
C07 = 0xC9 0xE8 0x81 0x9D 0xC7 0x3B 0xA5 0xAE 0x50 0xF5 0xB5 0x70 0x56 0x1A 0x6A 0x07 
C08 = 0xF6 0x59 0x36 0x16 0xE6 0x05 0x56 0x89 0xAD 0xFB 0xA1 0x80 0x27 0xAA 0x2A 0x08 
C09 = 0x98 0xFB 0x40 0x64 0x8A 0x4D 0x2C 0x31 0xF0 0xDC 0x1C 0x90 0xFA 0x2E 0xBE 0x09 
C10 = 0x2A 0xDE 0xDA 0xF2 0x3E 0x95 0xA2 0x3A 0x17 0xB5 0x18 0xA0 0x5E 0x61 0xC1 0x0A 
C11 = 0x44 0x7C 0xAC 0x80 0x52 0xDD 0xD8 0x82 0x4A 0x92 0xA5 0xB0 0x83 0xE5 0x55 0x0B 
C12 = 0x8D 0x94 0x2D 0x1D 0x95 0xE6 0x7D 0x2C 0x1A 0x67 0x10 0xC0 0xD5 0xFF 0x3F 0x0C 
C13 = 0xE3 0x36 0x5B 0x6F 0xF9 0xAE 0x07 0x94 0x47 0x40 0xAD 0xD0 0x08 0x7B 0xAB 0x0D 
C14 = 0x51 0x13 0xC1 0xF9 0x4D 0x76 0x89 0x9F 0xA0 0x29 0xA9 0xE0 0xAC 0x34 0xD4 0x0E 
C15 = 0x3F 0xB1 0xB7 0x8B 0x21 0x3E 0xF3 0x27 0xFD 0x0E 0x14 0xF0 0x71 0xB0 0x40 0x0F 
C16 = 0x2F 0xB2 0x6C 0x2C 0x0F 0x0A 0xAC 0xD1 0x99 0x35 0x81 0xC3 0x4E 0x97 0x54 0x10 
C17 = 0x41 0x10 0x1A 0x5E 0x63 0x42 0xD6 0x69 0xC4 0x12 0x3C 0xD3 0x93 0x13 0xC0 0x11 
C18 = 0xF3 0x35 0x80 0xC8 0xD7 0x9A 0x58 0x62 0x23 0x7B 0x38 0xE3 0x37 0x5C 0xBF 0x12 
C19 = 0x9D 0x97 0xF6 0xBA 0xBB 0xD2 0x22 0xDA 0x7E 0x5C 0x85 0xF3 0xEA 0xD8 0x2B 0x13 
C20 = 0x54 0x7F 0x77 0x27 0x7C 0xE9 0x87 0x74 0x2E 0xA9 0x30 0x83 0xBC 0xC2 0x41 0x14 
C21 = 0x3A 0xDD 0x01 0x55 0x10 0xA1 0xFD 0xCC 0x73 0x8E 0x8D 0x93 0x61 0x46 0xD5 0x15 
C22 = 0x88 0xF8 0x9B 0xC3 0xA4 0x79 0x73 0xC7 0x94 0xE7 0x89 0xA3 0xC5 0x09 0xAA 0x16 
C23 = 0xE6 0x5A 0xED 0xB1 0xC8 0x31 0x09 0x7F 0xC9 0xC0 0x34 0xB3 0x18 0x8D 0x3E 0x17 
C24 = 0xD9 0xEB 0x5A 0x3A 0xE9 0x0F 0xFA 0x58 0x34 0xCE 0x20 0x43 0x69 0x3D 0x7E 0x18 
C25 = 0xB7 0x49 0x2C 0x48 0x85 0x47 0x80 0xE0 0x69 0xE9 0x9D 0x53 0xB4 0xB9 0xEA 0x19 
C26 = 0x05 0x6C 0xB6 0xDE 0x31 0x9F 0x0E 0xEB 0x8E 0x80 0x99 0x63 0x10 0xF6 0x95 0x1A 
C27 = 0x6B 0xCE 0xC0 0xAC 0x5D 0xD7 0x74 0x53 0xD3 0xA7 0x24 0x73 0xCD 0x72 0x01 0x1B 
C28 = 0xA2 0x26 0x41 0x31 0x9A 0xEC 0xD1 0xFD 0x83 0x52 0x91 0x03 0x9B 0x68 0x6B 0x1C 
C29 = 0xCC 0x84 0x37 0x43 0xF6 0xA4 0xAB 0x45 0xDE 0x75 0x2C 0x13 0x46 0xEC 0xFF 0x1D 
C30 = 0x7E 0xA1 0xAD 0xD5 0x42 0x7C 0x25 0x4E 0x39 0x1C 0x28 0x23 0xE2 0xA3 0x80 0x1E 
C31 = 0x10 0x03 0xDB 0xA7 0x2E 0x34 0x5F 0xF6 0x64 0x3B 0x95 0x33 0x3F 0x27 0x14 0x1F 
C32 = 0x5E 0xA7 0xD8 0x58 0x1E 0x14 0x9B 0x61 0xF1 0x6A 0xC1 0x45 0x9C 0xED 0xA8 0x20

Для удобства их можно записать в массив, но последующая реализация в данной заметке использует генерацию во время работы программы.

Реализация

В реализации используется понятие «чанк» — один блок размером 128 бит (16 байт), созданный с помощью массива из двух беззнаковых целых по 64 бита:

// Длинна блока в байтах(16 байт = 128 бит)
#define KUZNECHIK_BLOCK_SIZE 16

// Один блок (чанк) задается как массив двух беззнаковых целых по 64 бита
typedef uint64_t chunk[2];

Важное замечание: так как чанк является по своей сути массивом, то для передачи в функцию адреса массива не требуется дополнительный указатель.

Таблицы нелинейных и вектор линейного преобразований:

// Таблица прямого нелинейного преобразования согластно ГОСТ 34.12-2015
const uint8_t Pi[] = {
    0xFC, 0xEE, 0xDD, 0x11, 0xCF, 0x6E, 0x31, 0x16, 0xFB, 0xC4, 0xFA, 0xDA, 0x23, 0xC5, 0x04, 0x4D,
    0xE9, 0x77, 0xF0, 0xDB, 0x93, 0x2E, 0x99, 0xBA, 0x17, 0x36, 0xF1, 0xBB, 0x14, 0xCD, 0x5F, 0xC1,
    0xF9, 0x18, 0x65, 0x5A, 0xE2, 0x5C, 0xEF, 0x21, 0x81, 0x1C, 0x3C, 0x42, 0x8B, 0x01, 0x8E, 0x4F,
    0x05, 0x84, 0x02, 0xAE, 0xE3, 0x6A, 0x8F, 0xA0, 0x06, 0x0B, 0xED, 0x98, 0x7F, 0xD4, 0xD3, 0x1F,
    0xEB, 0x34, 0x2C, 0x51, 0xEA, 0xC8, 0x48, 0xAB, 0xF2, 0x2A, 0x68, 0xA2, 0xFD, 0x3A, 0xCE, 0xCC,
    0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, 0xBF, 0x72, 0x13, 0x47, 0x9C, 0xB7, 0x5D, 0x87,
    0x15, 0xA1, 0x96, 0x29, 0x10, 0x7B, 0x9A, 0xC7, 0xF3, 0x91, 0x78, 0x6F, 0x9D, 0x9E, 0xB2, 0xB1,
    0x32, 0x75, 0x19, 0x3D, 0xFF, 0x35, 0x8A, 0x7E, 0x6D, 0x54, 0xC6, 0x80, 0xC3, 0xBD, 0x0D, 0x57,
    0xDF, 0xF5, 0x24, 0xA9, 0x3E, 0xA8, 0x43, 0xC9, 0xD7, 0x79, 0xD6, 0xF6, 0x7C, 0x22, 0xB9, 0x03,
    0xE0, 0x0F, 0xEC, 0xDE, 0x7A, 0x94, 0xB0, 0xBC, 0xDC, 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A,
    0xA7, 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, 0xB8, 0x38, 0x82, 0x64, 0x9F, 0x26, 0x41,
    0xAD, 0x45, 0x46, 0x92, 0x27, 0x5E, 0x55, 0x2F, 0x8C, 0xA3, 0xA5, 0x7D, 0x69, 0xD5, 0x95, 0x3B,
    0x07, 0x58, 0xB3, 0x40, 0x86, 0xAC, 0x1D, 0xF7, 0x30, 0x37, 0x6B, 0xE4, 0x88, 0xD9, 0xE7, 0x89,
    0xE1, 0x1B, 0x83, 0x49, 0x4C, 0x3F, 0xF8, 0xFE, 0x8D, 0x53, 0xAA, 0x90, 0xCA, 0xD8, 0x85, 0x61,
    0x20, 0x71, 0x67, 0xA4, 0x2D, 0x2B, 0x09, 0x5B, 0xCB, 0x9B, 0x25, 0xD0, 0xBE, 0xE5, 0x6C, 0x52,
    0x59, 0xA6, 0x74, 0xD2, 0xE6, 0xF4, 0xB4, 0xC0, 0xD1, 0x66, 0xAF, 0xC2, 0x39, 0x4B, 0x63, 0xB6
};

// Таблица обратного нелинейного преобразования
static const uint8_t Pi_reverse[] = {
    0xA5, 0x2D, 0x32, 0x8F, 0x0E, 0x30, 0x38, 0xC0, 0x54, 0xE6, 0x9E, 0x39, 0x55, 0x7E, 0x52, 0x91,
    0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, 0xA8, 0xD1, 0x29, 0xC6, 0xA4, 0x3F,
    0xE0, 0x27, 0x8D, 0x0C, 0x82, 0xEA, 0xAE, 0xB4, 0x9A, 0x63, 0x49, 0xE5, 0x42, 0xE4, 0x15, 0xB7,
    0xC8, 0x06, 0x70, 0x9D, 0x41, 0x75, 0x19, 0xC9, 0xAA, 0xFC, 0x4D, 0xBF, 0x2A, 0x73, 0x84, 0xD5,
    0xC3, 0xAF, 0x2B, 0x86, 0xA7, 0xB1, 0xB2, 0x5B, 0x46, 0xD3, 0x9F, 0xFD, 0xD4, 0x0F, 0x9C, 0x2F,
    0x9B, 0x43, 0xEF, 0xD9, 0x79, 0xB6, 0x53, 0x7F, 0xC1, 0xF0, 0x23, 0xE7, 0x25, 0x5E, 0xB5, 0x1E,
    0xA2, 0xDF, 0xA6, 0xFE, 0xAC, 0x22, 0xF9, 0xE2, 0x4A, 0xBC, 0x35, 0xCA, 0xEE, 0x78, 0x05, 0x6B,
    0x51, 0xE1, 0x59, 0xA3, 0xF2, 0x71, 0x56, 0x11, 0x6A, 0x89, 0x94, 0x65, 0x8C, 0xBB, 0x77, 0x3C,
    0x7B, 0x28, 0xAB, 0xD2, 0x31, 0xDE, 0xC4, 0x5F, 0xCC, 0xCF, 0x76, 0x2C, 0xB8, 0xD8, 0x2E, 0x36,
    0xDB, 0x69, 0xB3, 0x14, 0x95, 0xBE, 0x62, 0xA1, 0x3B, 0x16, 0x66, 0xE9, 0x5C, 0x6C, 0x6D, 0xAD,
    0x37, 0x61, 0x4B, 0xB9, 0xE3, 0xBA, 0xF1, 0xA0, 0x85, 0x83, 0xDA, 0x47, 0xC5, 0xB0, 0x33, 0xFA,
    0x96, 0x6F, 0x6E, 0xC2, 0xF6, 0x50, 0xFF, 0x5D, 0xA9, 0x8E, 0x17, 0x1B, 0x97, 0x7D, 0xEC, 0x58,
    0xF7, 0x1F, 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, 0x87, 0xDC, 0xE8, 0x4F, 0x1D, 0x4E, 0x04,
    0xEB, 0xF8, 0xF3, 0x3E, 0x3D, 0xBD, 0x8A, 0x88, 0xDD, 0xCD, 0x0B, 0x13, 0x98, 0x02, 0x93, 0x80,
    0x90, 0xD0, 0x24, 0x34, 0xCB, 0xED, 0xF4, 0xCE, 0x99, 0x10, 0x44, 0x40, 0x92, 0x3A, 0x01, 0x26,
    0x12, 0x1A, 0x48, 0x68, 0xF5, 0x81, 0x8B, 0xC7, 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, 0xD7, 0x74
};

// Вектор линейного преобразования
const uint8_t linear_vector[] = {
    0x94, 0x20, 0x85, 0x10, 0xC2, 0xC0, 0x01, 0xFB,
    0x01, 0xC0, 0xC2, 0x10, 0x85, 0x20, 0x94, 0x01
};

Функция X выполняет операцию побитового сложения по модулю 2 (XOR):

void X(chunk a, chunk b, chunk c) 
{
    c[0] = a[0] ^ b[0];
    c[1] = a[1] ^ b[1];
}

Функция S реализует нелинейное преобразование путем замены байт в соответствии с таблицей нелинейного преобразования Pi:

// Функция S
void S(chunk in_out) 
{
    // Счетчик
    int i;
    // Переход к представлению в байтах
    uint8_t *byte = (int8_t*) in_out;
    for (i = 0; i < KUZNECHIK_BLOCK_SIZE; i++) 
    {
        byte[i] = Pi[byte[i]];
    }
}
// Обратная функция S
void S_reverse(chunk in_out) 
{
    // Счетчик
    int i;
    // Переход к представлению в байтах
    uint8_t *byte = (int8_t*) in_out;
    for (i = 0; i < KUZNECHIK_BLOCK_SIZE; i++) 
    {
        byte[i] = Pi_reverse[byte[i]];
    }
}

Функция выполняет умножение в поле Галуа, которое реализовано в функции GF_mult:

uint8_t GF_mult(uint8_t a, uint8_t b) 
{    
    uint8_t c = 0;
    while (b) 
    {        
        if (b & 1)
            c ^= a;
        a = (a << 1) ^ (a & 0x80 ? 0xC3 : 0x00);
        b >>= 1;
    }
    return c;
}

Для удобства тела цикла функции L выделена подфункция R:

// Функция R
void R(uint8_t *in_out) 
{
    // Счетчик
    int i;
    // Аккумулятор
    uint8_t acc = in_out[15];
    // Переход к представлению в байтах
    uint8_t *byte = (int8_t*) in_out;
    for (i = 14; i >= 0; i--) 
    {
        byte[i + 1] = byte[i];
        acc ^= GF_mult(byte[i], linear_vector[i]);
    }
    byte[0] = acc;
}
// Обратная функция R
void R_reverse(uint8_t *in_out) 
{
    // Счетчик
    int i;
    // Аккумулятор
    uint8_t acc = in_out[0];
    // Переход к представлению в байтах
    uint8_t *byte = (int8_t*) in_out;
    for (int i = 0; i < 15; i++) 
    {
        byte[i] = byte[i + 1];
        acc ^= GF_mult(byte[i], linear_vector[i]);
    }
    byte[15] = acc;
}

Реализация функции L:

// Функция L
void L(uint8_t* in_out) 
{
    // Счетчик
    int i;
    for (i = 0; i < KUZNECHIK_BLOCK_SIZE; i++) 
        R(in_out);
}
// Обратная функция L
void L_reverse(uint8_t *in_out) 
{
    // Счетчик
    int i;
    for (int i = 0; i < 16; i++)
        R_reverse(in_out);
}

Для генерации итерационных ключей используется функция gen_round_keys:

void gen_round_keys(uint8_t* key, chunk* round_keys) 
{
    // Счетчик
    int i;

    // Константы
    uint8_t cs[32][KUZNECHIK_BLOCK_SIZE] = {};

    // Генерация констант с помощью L-преобразования номера итерации
    for (i = 0; i < 32; i++) 
    {
        cs[i][15] = i + 1;
        L(cs[i]);
    print_chunk(cs[i]);
    }

    // Итерационные ключи (четный и нечетный)
    chunk ks[2] = {};
    // Разместим ключ шифрования
    // результат = итерационный ключ = (преобразование к указателю на чанк)[номер чанка][часть чанка]
    round_keys[0][0] = ks[0][0] = ((chunk*) key)[0][0];
    round_keys[0][1] = ks[0][1] = ((chunk*) key)[0][1];
    round_keys[1][0] = ks[1][0] = ((chunk*) key)[1][0];
    round_keys[1][1] = ks[1][1] = ((chunk*) key)[1][1];

    // Генерация оставшихся ключей с использованием констант
    for (i = 1; i <= 32; i++) 
    {
        // Новый ключ
        chunk new_key = {0};

        // Преобразование X
        // (void*) для избежания предупреждений о неверном типе, передаваемом в функцию
        X(ks[0], (void*)cs[i - 1], new_key);
        // Преобразование S
        S(new_key);
        // Преобразование L
        // (uint8_t*) для избежания предупреждений о неверном типе, передаваемом в функцию
        L((uint8_t*)&new_key);
        // Преобразование X
        X(new_key, ks[1], new_key);

        // Сдвигаем ключи
        ks[1][0] = ks[0][0];
        ks[1][1] = ks[0][1];

        // Записываем новый ключ
        ks[0][0] = new_key[0];
        ks[0][1] = new_key[1];

        // Каждую 8 итерацию сети Фейстеля за исключением нулевой запишем ключи
        if ((i > 0) && (i % 8 == 0)) 
        {
            round_keys[(i >> 2)][0] = ks[0][0];
            round_keys[(i >> 2)][1] = ks[0][1];

            round_keys[(i >> 2) + 1][0] = ks[1][0];
            round_keys[(i >> 2) + 1][1] = ks[1][1];
        }
    }
}

Функция шифрования:

// Поддерживает запись результата в исходный массив
void kuznechik_encrypt(chunk *round_keys, chunk in, chunk out) 
{
    // Счетчик
    int i;
    // Буфер
    chunk p;
    // Создадим копию входных данных
    memcpy(p, in, sizeof(chunk));
    // В течении 10 итераций
    for (i = 0; i < 10; i++) 
    {
        // Преобразование X
        X(p, round_keys[i], p);
        // Для всех итераций кроме последней
        if (i < 9)
        {
            // Преобразование S
            S(p);
            // Преобразование L
            L((uint8_t*)&p);
        }
    }
    // Копируем полученный результат
    memcpy(out, p, sizeof(chunk));
}

Функция расшифровки:

void kuznechik_decrypt(chunk *round_keys, chunk in, chunk out)
{
    // Счетчик
    int i;
    // Буфер
    chunk p;
    // Создадим копию входных данных
    memcpy(p, in, sizeof(chunk));

    // Преобразование X
    X(p, round_keys[9], p);
    for (i = 8; i >= 0; i--) 
    {
        // Преобразование L
        L_reverse((uint8_t*)&p);
        // Преобразование S
        S_reverse(p);
        // Преобразование X
        X(p, round_keys[i], p);
    }
    // Копируем полученный результат
    memcpy(out, p, sizeof(chunk));
}

Для отладки реализована функция, выполняющая побайтовую печать чанка:

void print_chunk(chunk p) 
{
    int i;
    for (i = 0; i < sizeof(chunk); i++) 
        printf("0x%02X ", ((uint8_t *)p)[i]);
        
    printf("\n");
}

Реализация функции main:

int main(int argc, char *argv[])
{
    // Ключ (256 бит = 32 байт)
    uint8_t key[] = {
        0x88,0x99,0xaa,0xbb,0xcc,0xdd,0xee,0xff,
        0x00,0x11,0x22,0x33,0x44,0x55,0x66,0x77,
        0xfe,0xdc,0xba,0x98,0x76,0x54,0x32,0x10,
        0x01,0x23,0x45,0x67,0x89,0xab,0xcd,0xef
    };

    // Итерационные ключи
    chunk round_keys[10] = {};  

    // Генерация итерационных ключей
    gen_round_keys(key, round_keys);

    // Вывод итерационных ключей
    int i;
    printf("Итерацционные ключи:\n");
    for (i = 0; i < 10; i++)
        print_chunk(round_keys[i]);

    // Открытые данные
    uint8_t data[KUZNECHIK_BLOCK_SIZE] = { 
        0x11,0x22,0x33,0x44,0x55,0x66,0x77,0x00,
        0xff,0xee,0xdd,0xcc,0xbb,0xaa,0x99,0x88 
    };

    // Вывод открытых данных
    printf("Открытые данные:\n");
    // (void*) для избежания предупреждений о неверном типе, передаваемом в функцию
    print_chunk((void*)data);

    // Зашифрованные данные
    chunk encrypted;

    // Шифрование
    // (void*) для избежания предупреждений о неверном типе, передаваемом в функцию
    kuznechik_encrypt(round_keys, (void*)data, encrypted);

    // Вывод зашифрованных данных
    printf("Зашифрованные данные:\n");
    print_chunk(encrypted);

    // Результат расшифровки
    chunk decrypted;

    // Расшифровка
    kuznechik_decrypt(round_keys, encrypted, decrypted);

    // Вывод зашифрованных данных
    printf("Расшифрованные данные:\n");
    print_chunk(decrypted);

    return 0;
}

Тестирование

Первый тест в соответствии с ГОСТ дает следующие результаты:

Ключ:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x11 0x22 0x33 0x44 0x55 0x66 0x77 
0xFE 0xDC 0xBA 0x98 0x76 0x54 0x32 0x10 0x01 0x23 0x45 0x67 0x89 0xAB 0xCD 0xEF
Итерационные ключи:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x11 0x22 0x33 0x44 0x55 0x66 0x77 
0xFE 0xDC 0xBA 0x98 0x76 0x54 0x32 0x10 0x01 0x23 0x45 0x67 0x89 0xAB 0xCD 0xEF 
0xDB 0x31 0x48 0x53 0x15 0x69 0x43 0x43 0x22 0x8D 0x6A 0xEF 0x8C 0xC7 0x8C 0x44 
0x3D 0x45 0x53 0xD8 0xE9 0xCF 0xEC 0x68 0x15 0xEB 0xAD 0xC4 0x0A 0x9F 0xFD 0x04 
0x57 0x64 0x64 0x68 0xC4 0x4A 0x5E 0x28 0xD3 0xE5 0x92 0x46 0xF4 0x29 0xF1 0xAC 
0xBD 0x07 0x94 0x35 0x16 0x5C 0x64 0x32 0xB5 0x32 0xE8 0x28 0x34 0xDA 0x58 0x1B 
0x51 0xE6 0x40 0x75 0x7E 0x87 0x45 0xDE 0x70 0x57 0x27 0x26 0x5A 0x00 0x98 0xB1 
0x5A 0x79 0x25 0x01 0x7B 0x9F 0xDD 0x3E 0xD7 0x2A 0x91 0xA2 0x22 0x86 0xF9 0x84 
0xBB 0x44 0xE2 0x53 0x78 0xC7 0x31 0x23 0xA5 0xF3 0x2F 0x73 0xCD 0xB6 0xE5 0x17 
0x72 0xE9 0xDD 0x74 0x16 0xBC 0xF4 0x5B 0x75 0x5D 0xBA 0xA8 0x8E 0x4A 0x40 0x43 
Открытые данные:
0x11 0x22 0x33 0x44 0x55 0x66 0x77 0x00 0xFF 0xEE 0xDD 0xCC 0xBB 0xAA 0x99 0x88 
Зашифрованные данные:
0x7F 0x67 0x9D 0x90 0xBE 0xBC 0x24 0x30 0x5A 0x46 0x8D 0x42 0xB9 0xD4 0xED 0xCD 
Расшифрованные данные:
0x11 0x22 0x33 0x44 0x55 0x66 0x77 0x00 0xFF 0xEE 0xDD 0xCC 0xBB 0xAA 0x99 0x88

Второй тест:

Ключ:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x11 0x22 0x33 0x44 0x55 0x66 0x77 
0xFE 0xDC 0xBA 0x98 0x76 0x54 0x32 0x10 0x01 0x23 0x45 0x67 0x89 0xBA 0xDC 0xEF
Итерационные ключи:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x11 0x22 0x33 0x44 0x55 0x66 0x77 
0xFE 0xDC 0xBA 0x98 0x76 0x54 0x32 0x10 0x01 0x23 0x45 0x67 0x89 0xAB 0xCD 0xEF 
0xDB 0x31 0x48 0x53 0x15 0x69 0x43 0x43 0x22 0x8D 0x6A 0xEF 0x8C 0xC7 0x8C 0x44 
0x3D 0x45 0x53 0xD8 0xE9 0xCF 0xEC 0x68 0x15 0xEB 0xAD 0xC4 0x0A 0x9F 0xFD 0x04 
0x57 0x64 0x64 0x68 0xC4 0x4A 0x5E 0x28 0xD3 0xE5 0x92 0x46 0xF4 0x29 0xF1 0xAC 
0xBD 0x07 0x94 0x35 0x16 0x5C 0x64 0x32 0xB5 0x32 0xE8 0x28 0x34 0xDA 0x58 0x1B 
0x51 0xE6 0x40 0x75 0x7E 0x87 0x45 0xDE 0x70 0x57 0x27 0x26 0x5A 0x00 0x98 0xB1 
0x5A 0x79 0x25 0x01 0x7B 0x9F 0xDD 0x3E 0xD7 0x2A 0x91 0xA2 0x22 0x86 0xF9 0x84 
0xBB 0x44 0xE2 0x53 0x78 0xC7 0x31 0x23 0xA5 0xF3 0x2F 0x73 0xCD 0xB6 0xE5 0x17 
0x72 0xE9 0xDD 0x74 0x16 0xBC 0xF4 0x5B 0x75 0x5D 0xBA 0xA8 0x8E 0x4A 0x40 0x43 
Открытые данные:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x77 0x66 0x55 0x44 0x33 0x22 0x11 
Зашифрованные данные:
0xE4 0xBA 0xC9 0x66 0xA4 0x9C 0xB8 0x01 0xB4 0xBB 0xAA 0xDC 0x10 0x57 0x38 0x2B 
Расшифрованные данные:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x77 0x66 0x55 0x44 0x33 0x22 0x11

Третий тест:

Ключ:
0x77 0x66 0x55 0x44 0x33 0x22 0x11 0x00 0xFF 0xEE 0xDD 0xCC 0xBB 0xAA 0x99 0x88 
0xEF 0xCD 0xAB 0x89 0x67 0x45 0x23 0x01 0x10 0x32 0x54 0x76 0x98 0xBA 0xDC 0xFE
Итерационные ключи:
0x77 0x66 0x55 0x44 0x33 0x22 0x11 0x00 0xFF 0xEE 0xDD 0xCC 0xBB 0xAA 0x99 0x88 
0xEF 0xCD 0xAB 0x89 0x67 0x45 0x23 0x01 0x10 0x32 0x54 0x76 0x98 0xBA 0xDC 0xFE 
0x14 0xC9 0xB7 0xB2 0xB3 0xCA 0x26 0x5D 0xFE 0x64 0x53 0x58 0x47 0x9D 0x10 0x3E 
0xF8 0x21 0xC1 0x62 0x83 0x09 0xAF 0xE1 0xAA 0xF2 0x06 0xF2 0x36 0x9B 0x26 0x6A 
0xC0 0x87 0x03 0x08 0x56 0xD9 0x6C 0xF3 0x43 0x88 0x12 0x61 0x5E 0x1B 0xCC 0x9B 
0x5B 0x86 0x07 0xAC 0xDE 0x79 0x53 0x88 0xE7 0x36 0x17 0x5A 0x9D 0x40 0xF8 0x74 
0xD4 0x51 0xAE 0x46 0xCD 0xBE 0x34 0x2B 0x97 0xFE 0x8A 0x72 0xDB 0xC8 0x48 0x93 
0x78 0x39 0xED 0xCA 0x72 0xCA 0x57 0x9E 0xFE 0x5A 0x64 0xFF 0x03 0xE1 0xDC 0x12 
0xA3 0x5B 0x90 0x35 0x43 0x5E 0x38 0x09 0x46 0x4D 0xED 0x01 0x31 0x77 0xAA 0xAB 
0x0E 0xB4 0x73 0x8D 0x85 0x93 0x91 0x99 0xBE 0xCE 0x10 0x92 0x37 0x31 0x91 0x4C 
Открытые данные:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x77 0x66 0x55 0x44 0x33 0x22 0x11 
Зашифрованные данные:
0xDF 0x4B 0x25 0x6B 0x59 0xD4 0x99 0xA5 0x52 0xB7 0x7E 0xF7 0x4C 0x59 0x0B 0x8B 
Расшифрованные данные:
0x88 0x99 0xAA 0xBB 0xCC 0xDD 0xEE 0xFF 0x00 0x77 0x66 0x55 0x44 0x33 0x22 0x11

Вывод

В данной заметке были разобраны алгоритм шифрования Кузнечик и теоретическая база, используемая в его основе, была разработана программа на языке Си.

Текст программы на языке Си доступен в репозитории C_Kuznechik_GOST_R_34.12-2015.