Введение
Заметка оперирует терминами скаляр и вектор, а так же операциями над ними, что требует от читателя понимания векторной алгебры.
Важное примечание: для обозначения операций используются символы:
- векторное произведение A × B = вектор;
- скалярное произведение A • B = скаляр;
- покомпонентное произведение (Адамара) A ∘ B = вектор;
- произведение вектора и скаляра A * b = вектор.
В теории существуют четыре основных типа источников света:
- фоновое (ambient) — нулевая отметка при расчете освещения, обеспечивающая равномерное освещение при отсутствии других источников;
- точечное (omni) — точка в пространстве, которая светит одинаково во все стороны;
- прожектор (spot) — точечный источник, ограниченный конусом, задающим направление;
- направленное (direct) — бесконечно далеко удаленная точка, лучи которой идут параллельно (упрощает расчет освещения) благодаря расстоянию до неё.
Популярные модели освещения, используемые в трехмерных приложениях:
- плоское затенение (flat shading);
- затенение по Гуро (Gouraud/smooth shading);
- затенение по Фонгу (Phong shading);
- затенение Блинна-Фонга (Blinn-Phong shading);
- карты освещения (light map);
- освещение на основе изображения (image-based lighting);
- непрямое освещение на основе световых проб (probe-based indirect lighting);
- окружающее преграждение в пространстве экрана (screen-space ambient occlusion, SSAO).
Методы предложенные выше не подходят для рендера теней, для этого используются:
- проецирование теней (transforming polygons to ground, TPG);
- карты теней (shadow mapping, shadow Z-buffer calculation);
- каскадные карты теней (cascaded shadow maps, CSM);
- отражающие карты теней (reflective shadow maps, RSM).
Отдельной темой является трассировка лучей (ray tracing), получившая развитие благодаря компании Nvidia, но ей будет посвящена отдельная заметка.
Отражения
Согласно Фонгу, любой свет, падающий на поверхность, образует три вида отражений:
- диффузное (diffuse);
- зеркальное (specular);
- фоновое (ambient).
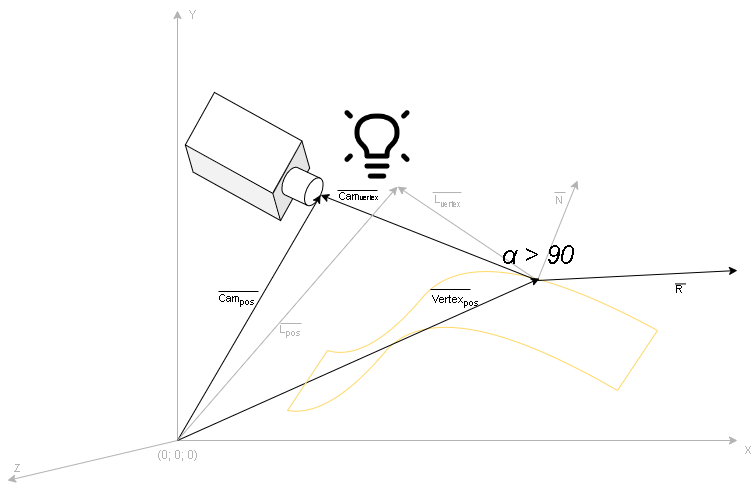
Далее представлены формулы, которые оперируют перемножением векторов. В последующих выражениях вычисляются следующие векторы: i — интенсивность свечения поверхности, k — коэффициент по цветам, который учитывает свойства материала поверхности. i light — интенсивность излучения источника образуемый из цвета и удаленности от поверхности.
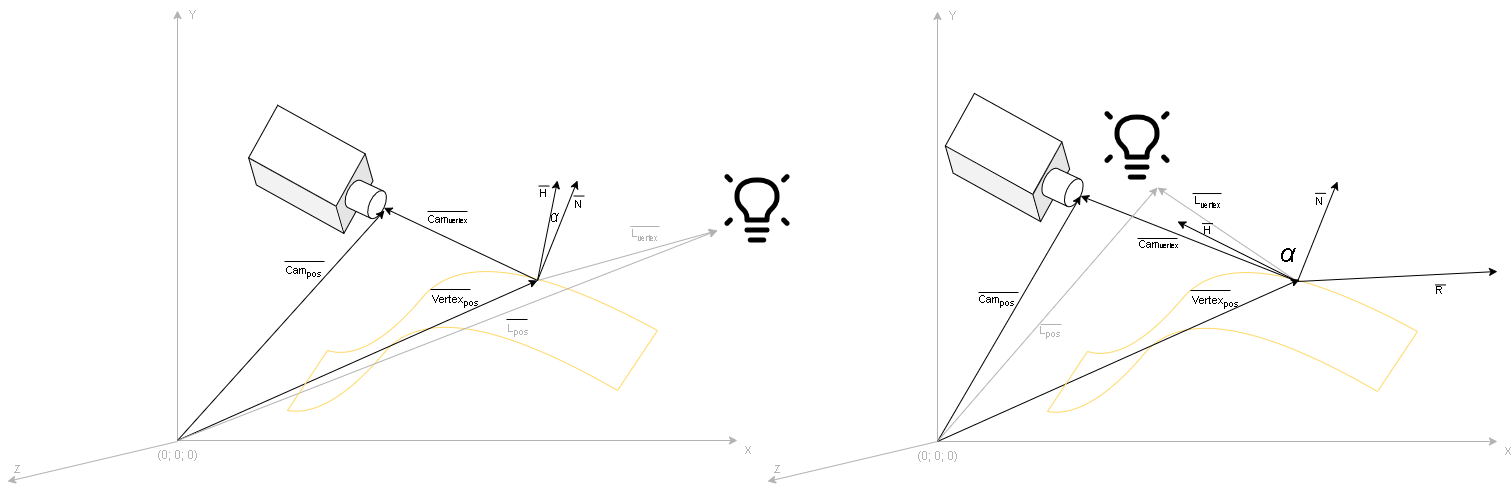
Расположение векторов для вычисления отражений относительно желтой поверхности представлено на рисунке 1.
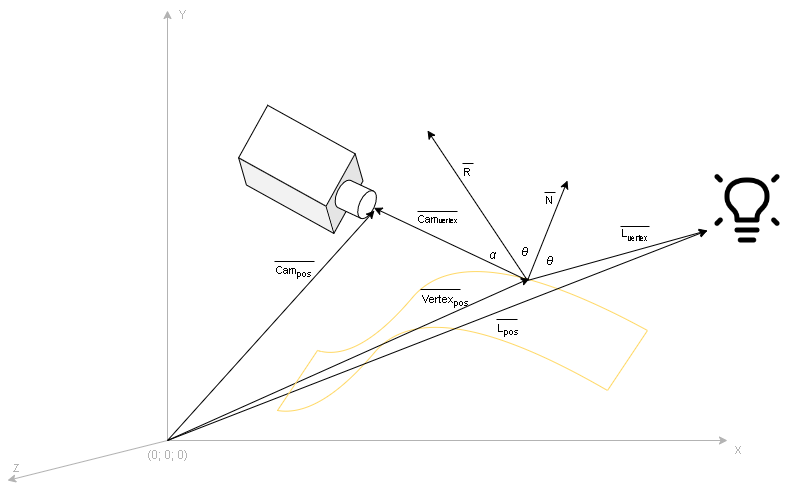
На рисунке 1 изображены векторы:
- Vertexpos — трансформированная позиция вершины в пространстве;
- Campos — позиция камеры в пространстве;
- Camvertex — позиция камеры относительно вершины = Campos ₋ Vertexpos;
- Lpos — позиция источника света в пространстве;
- Lvertex — позиция источника света относительно вершины = Lpos ₋ Vertexpos;
- N — нормаль поверхности (по рисунку трансформированная);
- R — вектор отраженного луча.
Важное замечание: на рисунке изображены не нормализованные вектора, а в процессе вычислений их необходимо нормализовать.
Итоговая освещенность поверхности вычисляется как сумма векторов:
i = i ambient + i diffuse + i specular
Для каждой компоненты может использоваться текстура, определяющая неоднородность:
i = i ambient ∘ textureambient + i diffuse ∘ texturediffuse+ i specular ∘ texturespecular
Диффузное отражение
Этот вид отражения характеризуется матовостью поверхности. Матовой или Ламбертовой поверхностью называется поверхность, шероховатость которой настолько велика, что падающий луч рассеивается равномерно во все стороны. Такие поверхности обладают собственным отражаемым цветом, который характеризует отражаемые и поглощаемые цвета источников. Например: цвет поверхности не имеет красной компоненты и при освещении красным источником поверхность будет иметь черный цвет, так как весь красный диапазон был ей поглощен.
Интенсивность диффузной составляющей отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью поверхности:
i diffuse = kdiffuse ∘ i light * cos(θ),
где θ — угол между нормалью в точке падения луча и его вектором, а kdiffuse — вектор с коэффициентами диффузного отражения, которые задают количество отраженного света поверхностью для каждой составляющей цвета [0.0;1.0].
Данную формулу можно упростить для графических устройств, используя скалярное перемножение:
i diffuse = kdiffuse ∘ i light * (Lvertex • N),
где Lvertex — вектор расположения источника освещения, а N — вектор нормали к поверхности
Зеркальное отражение
Поверхность считается идеально зеркальной, если глубина её шероховатостей (h) много меньше длинны волны отражаемого света (λ) ~ 0.5 мкм.
Собственный цвет в данном виде отражения не используется и в качестве kspecular следует вектор с компонентами в диапазоне [0.0;1.0], которое характеризует отражаемую часть потока.
Интенсивность зеркального отражения вычисляется используя эмпирическую модель Фонга:
i specular = kspecular ∘ i light * cosp(α),
где α — угол отклонения от линии идеального отражения луча, p — показатель глянцевости (glossiness), в библиотеке материалов WaveFront — Ns (specular exponent).
Важное замечание: показатель глянцевости в библиотеках mtl имеет диапазон от 0 до 1000, где значение Ns = 1000 является максимальным показателем глянцевости, что в формуле p должно равняться 1, а с уменшением Ns требуется увеличивать p
Малые значения показателя глянцевости (<100) соответствуют материалам с обычными оптическими свойствами, а значения в диапазоне от 100 до 500 соответствуют оптическим свойствам металлических поверхностей.
Вычисления можно упростить:
i specular = i light ∘ kspecular * (Camvertex • R)p,
где R — отражение отрицательного значения вектора света, Camvertex — вектор, направленный к зрителю.
Примечание: в GLSL для вычисления вектора R используется функция reflect.
Фоновое отражение
Фоновое отражение связано с фоновым источником света. В большинстве сцен реальной жизни, где есть хотя бы один источник света, базовая освещенность всех предметов имеет ненулевое значение благодаря множественным отражениям света от поверхности. Вычисляется фоновое отражение просто:
i ambient = kambient ∘ i light,
где kambient — вектор, хранящий цвета окружающего освещения [0.0;1.0]. Для неоднородно освещенных объектов можно использовать текстуру окружения.
Модели освещения
Плоское затенение
Плоское затенение применяется единым уровнем ко всему фрагменту. Сперва уровень освещенности вычисляется в каждой вершине, затем полученные значения усредняются и весь фрагмент окрашивается с учетом данного результата. Пример данного способа изображен на рисунке 2.
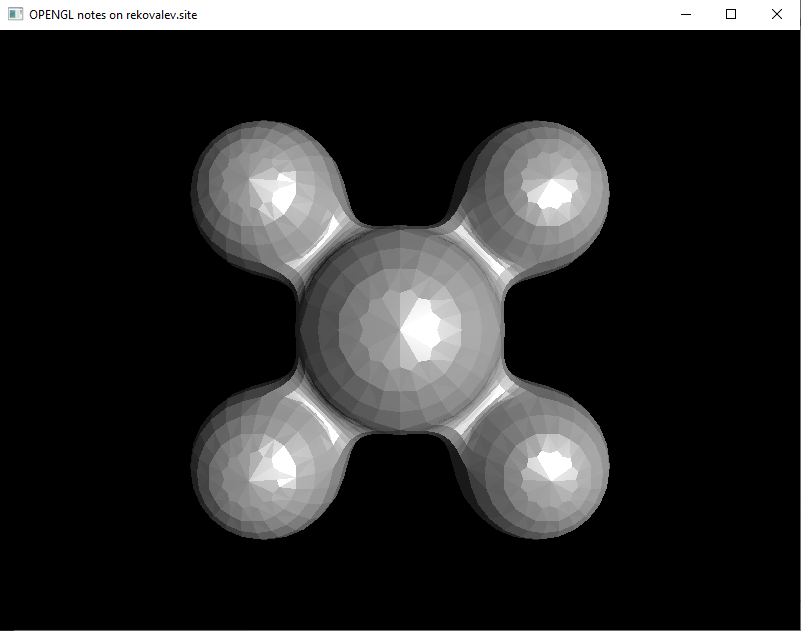
На основании рисунка 2 можно отметить что данная модель освещения весьма грубая и позволяет незначительно увеличить реалистичность результата за счет повышения числа фрагментов, что ведет к повышению стоимости рендера.
Для получения такого эффекта на вершинном шейдере необходимо подготовить для фрагментного данные о положении в пространстве:
- трансформированной вершины (Vertexpos) — умножить матрицу трансформации модели на вектор положения вершины (приведение к мировым координатам);
- источника света относительно вершины (Lvertex) — вычесть из вектора положения источника света вектор трансформированной вершины;
- камеры относительно вершины (Camvertex) — вычесть из вектора положения камеры вектор трансформированной вершины.
Из данных о вершине можно получить вектор нормали с помощью векторного произведения результатов функций dFdx и dFdy от полученной вершины. Результат векторного перемножения необходимо нормализировать. Такой подход позволяет добиться единой нормали для фрагмента.
Функции dFdx и dFdy возвращают вектор частной производную относительно координат окна.
Для расчета яркости необходимо посчитать скалярное произведение между вектором падения луча и нормалью фрагмента:
Nflat = dFdx(Vertexpos) × dFdy(Vertexpos)
i diffuse = kdiffuse ∘ i light * (Lvertex • Nflat)
Для расчета блика необходимо получить обратный вектор отражения. Данный вектор используется в скалярном произведении с вектором камеры, которое возводится в степень показателя глянцевости:
R = -reflect(Lvertex, Nflat)
i specular = i light ∘ kspecular * (R • Camvertex)p
Вторым возможным вариантом получения эффекта плоского затенения в GLSL является передача нормалей в фрагментный шейдер с параметром flat, отключающим интерполяцию. Данный вариант более предпочтителен ибо выигрывает по производительности и легко получается из затенений Гуро или Фонга. Результат работы второго варианта получается более резким и представлен на рисунке 3.
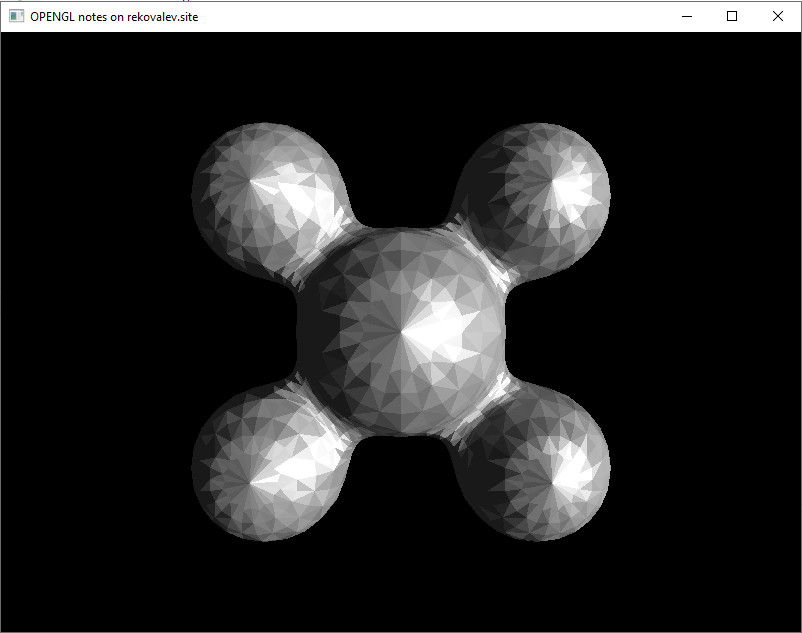
Затенение по Гуро
Данный метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде полигональной сетки с плоскими гранями, путем интерполяции цветов примыкающих граней. В данной модели освещение не усредняется для фрагмента, а линейно интерполируется между вершинами. Результат работы метода представлен на рисунке 4.
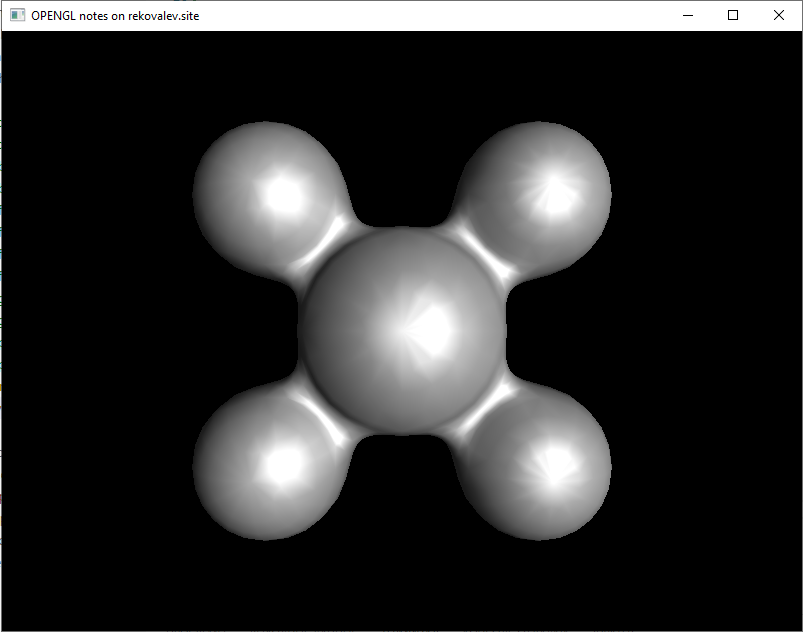
Исходя из результатов на рисунке 2 можно отметить смазанность блика (эффект «снежинки»), который может теряться при уменьшении уровня детализации.
В данном способе большая часть вычислений производится в вершинном шейдере:
- трансформированной вершины (Vertexpos) — умножить матрицу трансформации модели на вектор положения вершины (приведение к мировым координатам);
- трансформированной нормали (N) — умножить вектор нормали на матрицу трансформации модели (приведение к мировым координатам);
- источника света относительно вершины (Lvertex) — вычесть из вектора положения источника света вектор трансформированной вершины;
- камеры относительно вершины (Camvertex) — вычесть из вектора положения камеры вектор трансформированной вершины.
Фрагментному шейдеру передаются две интенсивности отражений:
- диффузная (diffuse);
- зеркальная (specular).
Для зеркальной составляющей требуется обратный отраженный вектор:
R = -reflect(Lvertex, N)
Диффузная и зеркальные составляющие вычисляются по ранее рассмотренным формулам:
i diffuse = kdiffuse ∘ i light * (Lvertex • N),
i specular = i light ∘ kspecular * (R • Camvertex)p
На фрагментном шейдере происходит добавление фонового отражения и смешивание с текстурами.
С оригинальной публикацией Гуро можно ознакомиться по ссылке.
Затенение по Фонгу
В модели Фонга между вершинами интерполируется нормаль. Освещенность участка вычисляется на фрагментном шейдере, благодаря чему изображение получается более качественным при использовании того же уровня детализации. Пример использования модели Фонга изображен на рисунке 5.
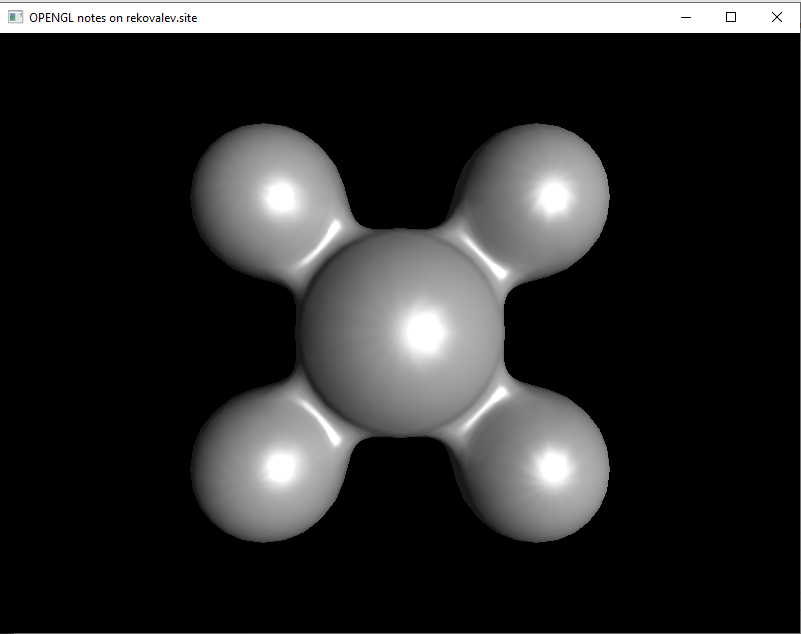
Для вычислений отражений необходимо передать фрагментному шейдеру:
- трансформированную нормаль (N) — умножить матрицу трансформации модели на вектор нормали (приведение к мировым координатам);
- положение источника света относительно вершины (Lvertex) — вычесть из вектора положения источника света вектор трансформированной вершины;
- положение камеры относительно вершины (Camvertex) — вычесть из вектора положения камеры вектор трансформированной вершины.
На фрагментном шейдере вычисляется обратный отраженный вектор для зеркальной составляющей:
R = -reflect(Lvertex, N)
Диффузная и зеркальные составляющие вычисляются по ранее рассмотренным формулам:
i diffuse = kdiffuse ∘ i light * (Lvertex • N),
i specular = i light ∘ kspecular * (R • Camvertex)p
После производится добавление фонового отражения и смешивание с текстурами.
С оригинальной публикацией Фонга можно ознакомиться по ссылке.
Затенение Блинна-Фонга
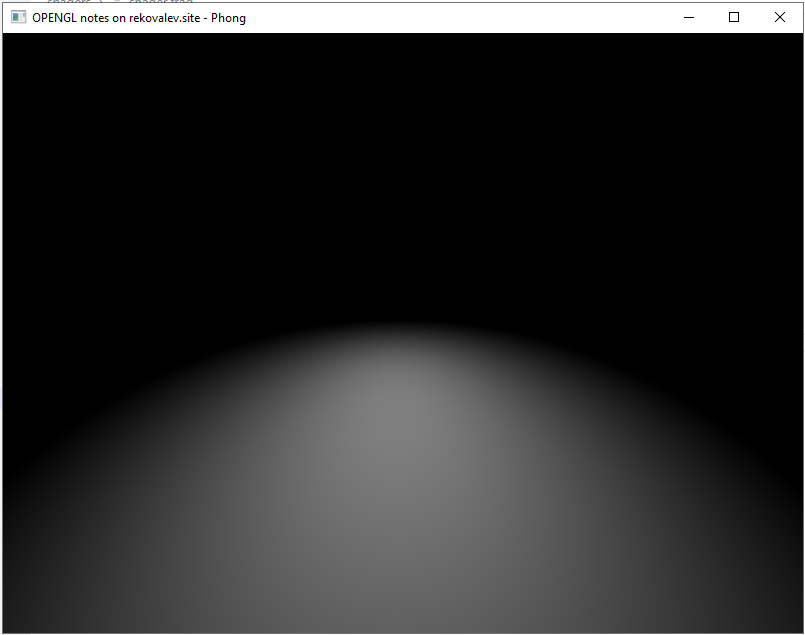
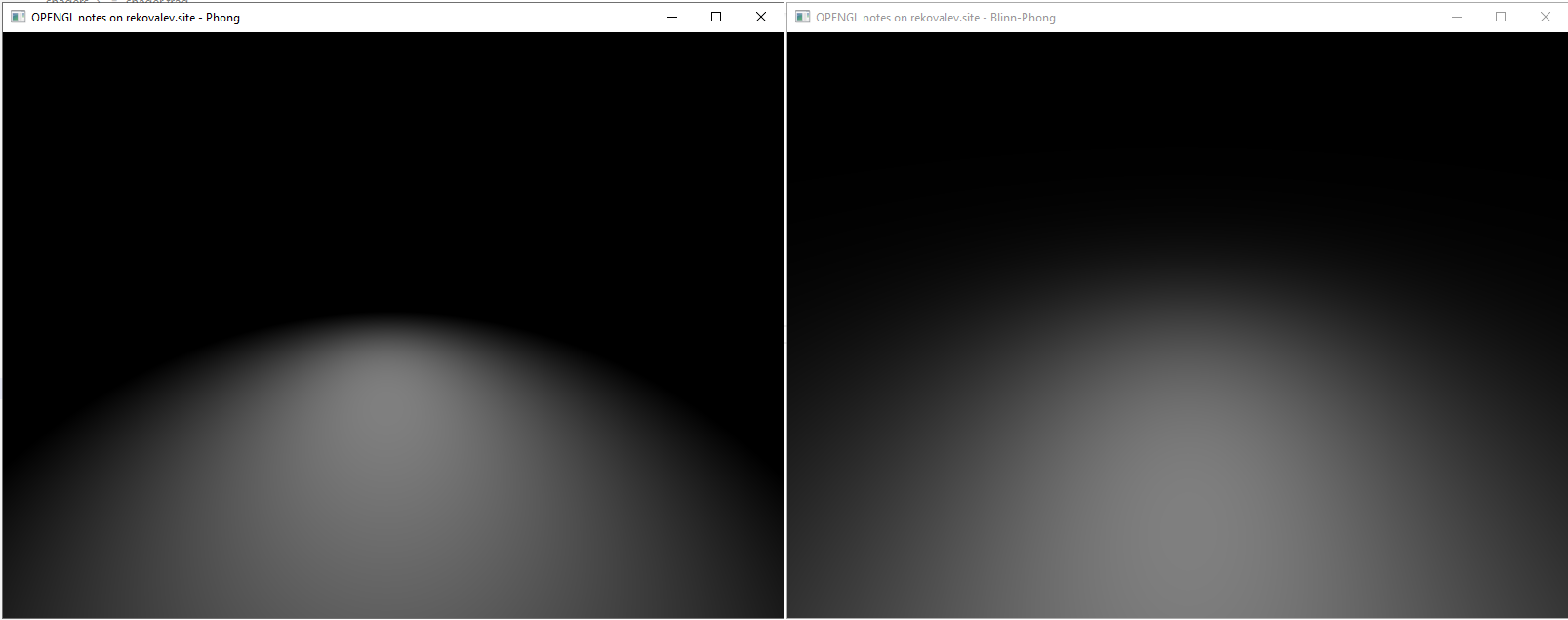
Предыдущие рассмотренные модели имеют недостаток: пропадание блика, если угол α (между векторами направлением камеры и отражения) больше 90 градусов, что делает косинус в скалярном произведении отрицательным и дальнюю границу блика более острой. Данная ситуация изображена на рисунке 6.
На рисунке 7 представлен блик зеркального отражения (диффузное и фоновое отключены) при координатах позиции камеры (0; 0; 0), источника света (0; 0.2; 5) и плоской поверхности с координатами (0; -3; 0) и показателем глянцевости (1; 1; 1)
В модели затенения Блинна-Фонга используется иной подход к расчету зеркальной компоненты: вектор отражения заменен на серединный вектор H (медианный, «половины пути», Halfway). Данный вектор можно получить разделив сумму векторов Lvertex и Camvertex на её длину (нормализованная сумма векторов):
H = (Lvertex + Camvertex) / || Lvertex + Camvertex || = normalize( Lvertex + Camvertex)
Данный вектор представлен на рисунке 8.
Формула вычисления интенсивности зеркального отражения меняет свой вид на:
i specular = i light ∘ kspecular * (N • H)p
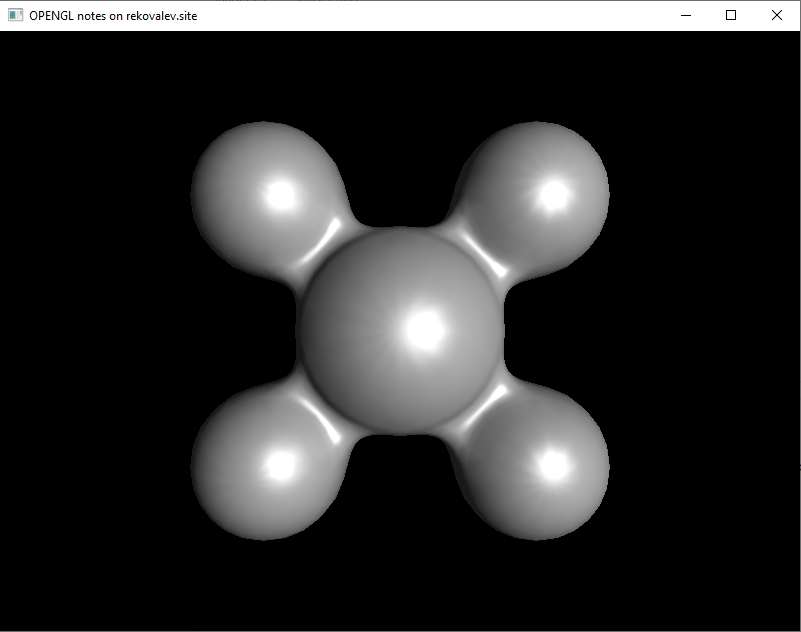
В среднем интенсивность при использовании медианного вектора больше, чем в случае с отраженным, следовательно показатель глянцевости должен отличаться в 4 раза. Результат с такой разницей представлен на рисунке 9.
На основании рисунка 9 можно сделать вывод, что блик имеет более реалистичную форму.
Результат работы метода Блинна-Фонга можно увидеть на рисунке 10.
С оригинальной публикацией Блинна можно ознакомиться по ссылке.
Карты освещения
Данная технология впервые появилась в игре Джона Кармака Quake в 1996 году, но до сих пор активно используется в различных игровых движках.
Идея заключается в предварительном расчете для статических объектов на сцене и запекания текстуры, учитывающей освещенность и отбрасываемые тени, что позволяет пропустить вычисления для объектов имеющих такие текстуры по отношению к статическим источникам света и повысить производительность.
Карты освещения могут отображать только рассеянное освещение и не могут использоваться для зеркальных поверхностей, поскольку они во многом зависят от положения камер. Например: хорошо подходят для бетонных поверхностей и плохо для металлического покрытия.
На рисунках 11 и 12 представлены сцена и её карта освещения.


Освещение на основе изображения
Техника Image-based lighting основана на создании кубической карты, которую можно использовать на глянцевых поверхностях для получения непрямого освещения.
Шесть граней кубической карты позволяют получить меняющиеся в зависимости от угла камеры отражения, которые захватывают происходящее за краями экрана. Для создания реалистичного отражения требуется большое разрешение граней, что в свою очередь требует затрат производительности и объема видеопамяти графического адаптера.
Проблем в производительности можно избежать, если использовать упрощенную версию сцены или считать её не каждый кадр.
Кубическая карта может создавать проблемы с перспективой в отражениях из-за того, что точка с которой ведется рендер мира не всегда совпадает с камерой.
Металлические объекты сложной формы не могут отражаться на собственных поверхностях, так как карта учитывает вклады в освещение только окружающих объектов.
Непрямое освещение на основе световых проб
Метод световых проб предназначен для решения проблем с видеопамятью и интерактивностью окружения имеющихся у техники на основе изображения.
Световая проба — альтернатива кубической карты с меньшим числом сторон и более низкого разрешения. На сцене размещается множество таких проб, для которых идет расчет освещенности.
Главный плюс данного метода в том, что световая проба занимает мало видеопамяти и как следствие их пересчет менее трудозатратен для графического устройства.
Результат сильно зависит от плотности расположения световых проб. В случае недостаточной плотности может создаваться прерывистое освещение.
Низкая детализация не позволяет использовать пробы для наложения теней.
С оригинальной публикацией Nvidia можно ознакомиться по ссылке.
Окружающее преграждение в пространстве экрана
Данный метод направлен на модификацию фоновой составляющей освещения, которая обычно принимается как константное значение. Одним из способов приближенного расчета затенения от непрямого освещения является алгоритм окружающего преграждения (ambient occlusion, AO), который имитирует ослабление непрямого освещения в окрестности углов, складок и прочих неровностей поверхностей.
Примечание: данный метод можно перевести как «фоновое затенение», но автор считает что это больше подходит под «ambient shading», а «occlusion» скорее про преграждение света другими объектами.
Алгоритмы расчета окружающего преграждения являются ресурсоемкими, поскольку требуют анализа окружающей геометрии. В 2007 году Crytek опубликовала работу с описанием алгоритма окружающего преграждения в пространстве экрана (SSAO).
Принцип, на котором основан алгоритм прост: для каждого фрагмента, присутствующего на экране, рассчитывается коэффициент преграждения (occlusion factor) на основе значений глубины окружающих элементов. Для получения коэффициента требуется сбор данных о глубине из сферической области, окружающей рассчитываемый фрагмент. Данные о глубине из сферической области сравниваются с глубиной рассчитываемого фрагмента. Число выборок из сферы, имеющих большую глубину, чем текущий фрагмент, определяют коэффициент затенения.
Реалистичность зависит от числа выборок в сфере. Большое число выборок требует больших затрат в производительности, а малое число выборок снижает точность алгоритма и приводит к появлению резких переходов между областями с различными коэффициентами затенения (banding). Для решения возникшей проблемы используется переориентация поворотом на случайный угол набора векторов выборок, что в свою очередь пораждает проблему шумового узора, который исправляется путем размытия.
Существует оптимизация путем использования «полусферы, ориентированной по нормали», которая исключает излишнее затенение благодаря игнорированию фрагментов, лежащих под поверхностью прилегающей к поверхности.
Пример вычисления выборок с использованием оптимизации путем использования полусферы представлен на рисунке 13.

Примечание: на рисунке 13 в качестве примера используется 21 выборка, но в реальных условиях этого недостаточно — увеличение числа выборок ведет к улучшению результата.
Для трансформации полусферы необходимо вычислить матрицу 3х3, состоящую из следующих векторов:
- tangent — разность случайного нормированного вектора и произведения нормали на скалярное произведение случайного вектора и нормали;
- bitangent — векторное произведение нормали и тангент-вектора;
- normal — нормаль точки на поверхности.
Формулы вычисления данных векторов:
tangent = randomVec — normal * randomVec · normal,
где randomVec — случайный нормированный вектор, а normal — нормированная нормаль.
bitangent = normal ⨯ tangent.
Полученная матрица умножается на выборку, для трансформации её в пространство полусферы, ориентированной по нормали.
Тени
Расчет теней в приложениях с использованием трехмерной графики является весьма трудоемким процессом.
Проецирование теней
Метод, предложенный Джимом Блинном в 1988 году, предоставляет уравнения для преобразования полигона в плоскость расположенную на y = 0, противоположную направлению, откуда падает свет. Рассматривается два вида источников света:
- свет в бесконечном удалении;
- местный источник света.
Источник света в бесконечности представлен на рисунке 14.
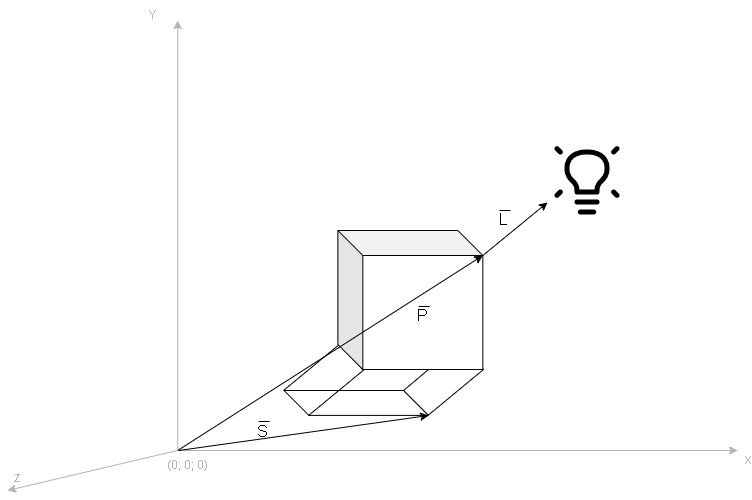
На рисунке 14 обозначены:
- удаленный источник света с координатами (xL, yL, zL);
- вершинная точка c координатами (xP, yP, zP);
- теневая точка (xS, yS, zS) — искомая.
Важное замечание: в оригинале считается zS = 0, так как именно ось Z расположена вертикально.
Из подобия треугольников имеем:
(xP — xS) / (zP — zs) = (xL — xP) / (zL — zP)
Решение для xS:
xS = (zP — zs) * (xL — xP) / (zL — zP)
Если L — вектор от точки, представленной вектором P, к источнику света, то точку тени, представленную вектором S, можно представить как:
S = P — a * L
Поскольку yS = 0, то имеем:
0 = yP — a * yL, из чего можно получить:
a = yP / yL
Вернувшись к xS, можно использовать:
xS = xP — (yP / yL) * xL
Для zS аналогично.
В матричной форме:
MS = { {1, 0, 0, 0}, {0, 1, 0, 0}, {-xL/zL, -yL/zL, 0, 0}, {0, 0, 0, 1} }
На рисунке 15 представлен локальный источник света.
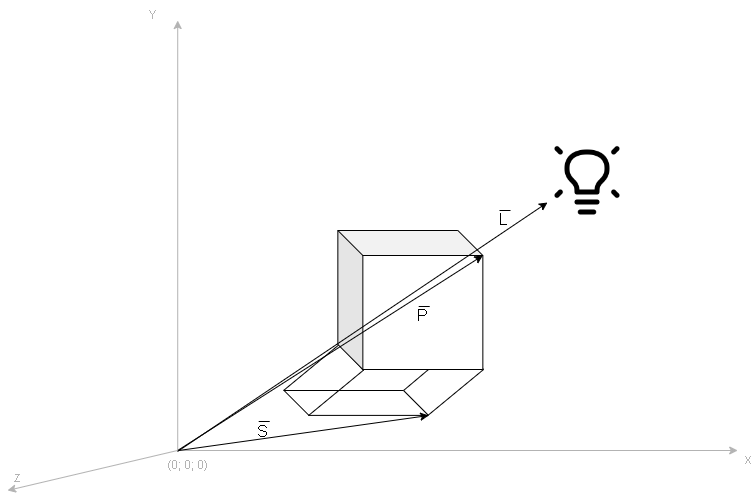
Если источник является локальным и представлен вектором L, идущим из начала координат, то необходимо определить вектор относительно вершины:
S = P — a * (P — L)
Используя, что yS = 0 имеем:
a = -yP / (yP — yL)
Вернувшись к xS, можно использовать:
xS = (xL*yP — xP*yL) / (yP — yL)
Для zS аналогично.
В матричной форме:
MS = { {-yL, 0, 0, 0}, {0, -yL, 0, 0}, {xL, yL, 0, 0}, {0, 0, 0, -yL} }
В обоих случаях преобразования можно производить:
S = P * MS
Данный метод имеет серьезный недостаток, так как проецирует тень только на землю (поверхность с нулевой высотой), но не требует дополнительной памяти и легко работает с любым числом источников света. Каждый полигон здесь рендерится N раз, где N — количество источников света.
Оригинальная публикация имеет название: Blinn, James F. “Me and My (Fake) Shadow”, доступная в IEEE. Computer Graphics and Applications, январь 1988, страницы 82-86 (не имеется в открытом доступе).
Карты теней
Данный метод также называется «Расчет теневого Z-буфера» или «вычисление теней на основании буфера глубины» и был описан Уильямсом в 1978г.
Важной проблемой нереалистичности теней является множественность источников и образование от некоторой площади. Проблема площади источника освещения представлена на рисунке 16.
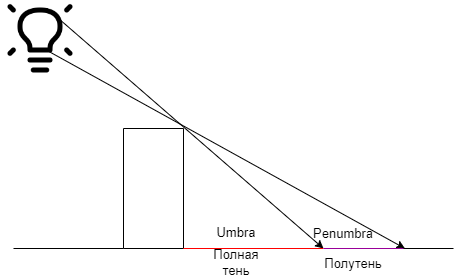
Исходя из рисунка 16 образуется два вида теней:
- полная тень (umbra);
- полутень (penumbra).
Граница между этими двумя видами теней обычно размыта. Рассматриваемый алгоритм позволяет решить данную задачу.
Алгоритм следует из представления о том, что теневые точки «спрятаны» от света. Другими словами: тени — это «скрытые поверхности» с точки зрения света. Если допустить, что точка освещения является точкой наблюдения (центром проекции), то можно визуализировать сцену с точки зрения источника света, используя Z-буфер для вычисления поверхностей, видимых для света. В результате Z-буфер будет содержать все точки, которые находятся ближе всего к источнику света. Любая точка, которая дальше по Z-буферу находится в тени.
Метод Z-буфера включает просмотр объекта с точки зрения каждого источника света в сцене и вычисление Z-буфера объекта видимого каждым источником света. Для каждого пикселя, видимого камерой, происходит преобразование к виду света, для определения, была ли видна данная точка свету.
При вычислении скрытых поверхностей для всех источников света интересна только информация о глубине, на основании которой может приниматься решение о расчете освещенности, что может ускорить рендеринг, при предварительном расчете теневых Z-буферов.
Основная проблема кроется в неточностях расчетов проекций, которые могут повлиять о решении освещенности точки. Помимо этого может возникнуть ситуация, когда точки затеняют сами себя. Допустимым решением является фильтрация на процент ближе, что обеспечивает дополнительное небольшое сглаживание краев теней. Возможны появления артефактов, связанных с разрешением теневых буферов.
Одни из самых распространенных артефактов — появление лесенок, называемого алиасинг (aliasing, элайсинг), которые можно исправить сглаживанием (antialiasing, антиалиасинг, антиэлайсинг). Такое явление в частности происходит при отображении большого числа пикселей из пространства сцены на один пиксель карты теней (perspective aliasing).
В отличии от предыдущего метода может использоваться для затенения любых сцен, но с выделением памяти под буферы источников света.
С оригинальной публикацией Уильямса можно ознакомиться по ссылке.
Каскадные карты теней
Метод каскадных карт теней является дополнением к методу карт теней и направлен на решение задач алиасинга. Можно заметить, что с постепенным отдалением от камеры данная проблема решается, следовательно для первого плана необходимо более высокое разрешение карт теней. Следовательно можно допустить разбиение карт теней на каскад, определяемый удаленностью от камеры. Первая карта каскада должна покрыть небольшой участок на том же количестве пикселей, что решает проблему перспективного алиасинга (perspective aliasing). По мере отдаления от камеры можно использовать больший участок.
Количество каскадов не ограничивается двумя, но часто применяется три: ближний (near), средний (middle) и дальний (far).
Дальнейшее рассмотрение ведется для перспективной камеры. Разбиение каскадов определяется усеченной пирамидой обзора, которая представлена на рисунке 17.
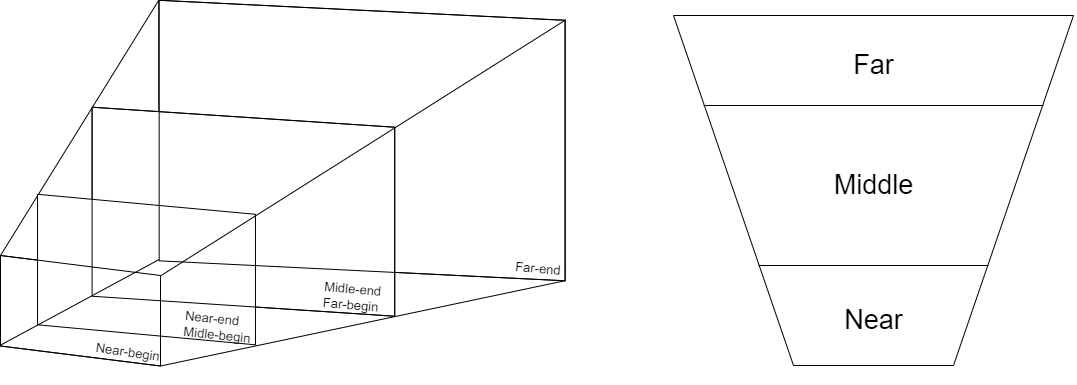
В рамках определенных каскадов необходимо создать ограничивающие рамки, которые будут основой для ортогональной проекции в теневом проходе. Они должны быть заданы в пространстве источника света (источник находится в нулях координатных осей и направлен вдоль оси Z).
Для восьми вершин увеченной пирамиды обзора необходимо найти координаты в пространстве обзора, согласно рисунку 18.
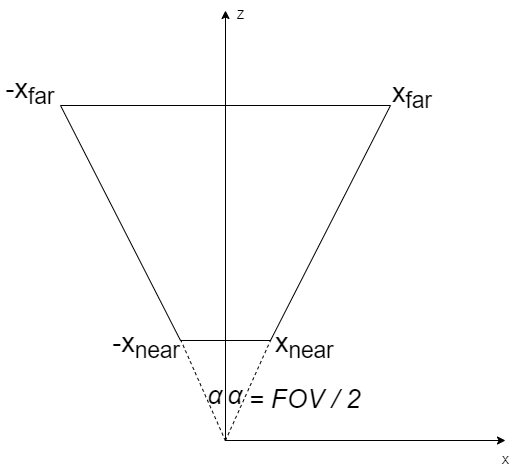
Координату xnear можно получить используя тригонометрические преобразования из малого треугольника, зная угол α = FOV / 2 и координату znear равную расстоянию до ближней плоскости (near):
xnear / znear = tan(α), из чего можно получить:
xnear = tan(α) * znear
Для xfar аналогично при zfar равной расстоянию до дальней плоскости (far):
xfar = tan(α) * zfar
Данные координаты из пространства камеры необходимо перенести в мировые координаты. Для этого обратимся к выражению для приведения координат вершины V из мировых (Vworld) к координатам камеры (Vview) с помощью матрицы вида (Mview):
Vview = Mview * Vworld, из чего можно получить:
Vworld = M-1view * Vview,
где M-1view — обратная матрица камеры.
Координаты усеченной пирамиды в мировом пространстве необходимо привести к пространству источника света. Для направленного источника достаточно просто повернуть сцену для того, чтобы источник света был направлен вдоль оси Z.
Из имеющихся координат каскадов в пространстве света можно получить границы рамок, задающих ортогональные проекции (максимальные и минимальные координаты восьми преобразованных точек).
С публикацией Nvidia можно ознакомиться по ссылке.
Отражающие карты теней
Данный алгоритм является расширением над простыми картами теней. Помимо хранения карты глубины для каждого пикселя, алгоритм сохраняет позиции в мировых координатах, нормали в мировых координатах и световую интенсивность источника освещения (в люменах).
Данные о световой интенсивности могут быть использованы для расчета непрямого освещения.
С оригинальной публикацией можно ознакомиться по ссылке.
Заключение
В данной заметке были рассмотрены различные техники расчета освещенности фрагментов в трехмерной графике и представлены формулы, используемые в расчетах.
В современных приложениях, занимающихся рендером трехмерной графики, используются различные комбинации описанных способов.