Введение
Заметка затрагивает тему кватернионов в срезе компьютерной графики в трехмерных приложений.
Кватернионы — это система гиперкомплексных чисел, образующая векторное пространство, которая может быть использована как способ описания вращения объекта в пространстве вокруг произвольной оси в пространстве. Открыты в 1843 г. У.Р. Гамильтоном. Подробнее данное определение будет раскрыто по пути рассмотрения связанной теории.
Под гиперкомплексными числами следует понимать обобщение понятия о числе, более широкое, чем обычные комплексные числа. Смысл обобщения состоит в том, чтобы обычные арифметические действия над такими числами одновременно выражали некоторые геометрические процессы в многомерном пространстве или давали количественное описание каких-либо физических законов.
Важное замечание: зачастую гиперкомплексные числа приравнивают к комплексным, но автор считает это не корректным.
Тема является весьма глубокой и для её понимания требуются базовые знания о матрицах, множествах и конкретно о комплексных числах, группах и телах. Автор постарается раскрыть большую часть определений, но при этом не создать бесконечную заметку. Часть теории здесь может быть не обязательной, но полезной для некоторых читателей для понимания математической картины, частью которой являются кватернионы.
Содержание заметки:
Коротко о множествах
Под множеством следует понимать совокупность объектов (элементов), которые понимаются как единое целое по конкретным признакам и критериям.
Для обозначения множеств используются заглавные латинские буквы, которые могут дополняться индексами. Например в школьной математике затрагивается множество натуральных чисел, которые используются для счета объектов и обозначаются:
\mathbb{N} = \{ 1, 2,3,…\}
Из этого множества выделяется подмножество \mathbb{P} простых чисел, имеющих только два делителя (единица и само число).
Над множествами возможны следующие операции:
- объединение: \mathbb{A} ∪ \mathbb{B} дает множество, содержащее все элементы из \mathbb{A} и \mathbb{B};
- разность: \mathbb{A} \ \mathbb{B} или \mathbb{A} - \mathbb{B} дает множество эл-тов \mathbb{A}, не входящих в \mathbb{B};
- дополнение: \setminus\mathbb{A} или \mathbb{-A} дает множество эл-тов, не входящих в \mathbb{A};
- пересечение: \mathbb{A} ∩ \mathbb{B} дает множество общих эл-тов для двух множеств.
Следует понимать следующие обозначения:
- \mathbb{A} ⊆ \mathbb{B} — нестрогое включение множества, когда каждый элемент мн-ва \mathbb{A} принадлежит так же мн-ву \mathbb{B}, но при этом множества могут быть равны;
- \mathbb{A} ⊂ \mathbb{B} — строгое включение множества, но при этом множество \mathbb{A} не может быть равно \mathbb{B};
- \mathbb{A} = \mathbb{B} — равенство двух множеств, которое может быть, если мн-ва \mathbb{A} и \mathbb{B} включены друг в друга: \mathbb{A}⊆\mathbb{B} и \mathbb{B}⊆\mathbb{A};
- 1 ∈ \mathbb{N} — 1 является элементом мн-ва \mathbb{N}.
Примечание: символ включения может быть отзеркален для обратной связи.
В целом для заметки потребуется понимание множеств над числами, где:
- \mathbb{Z} = \{ -∞, ..., -2, -1, 0, 1, 2, ..., ∞ \} — целые числа, дополнившие натуральные отрицательными значениями и нулем;
- \mathbb{Q} — рациональные числа или обыкновенные дроби, представленные в виде m / n, где m — целое число, называемое числителем, а n — натуральное, называемое знаменателем;
- \mathbb{I} — иррациональные числа, которые являются бесконечной непериодической десятичной дробью (их нельзя представить в виде обыкновенной дроби), например: √2, π (3.1415…), e (2.7182…) и т.д;
- \mathbb{R} — вещественные (действительные) числа, образованные объединением множеств рациональных и иррациональных чисел: \mathbb{R} = \mathbb{Q} ∪ \mathbb{I};
- \mathbb{C} — комплексные числа, о которых речь пойдет в следующем разделе;
- \mathbb{H} — кватернионы, являющиеся целью данной заметки.
Справедливо следующее выражение:
\mathbb{P} ⊂ \mathbb{N} ⊂ \mathbb{Z} ⊂ \mathbb{Q} ⊂ \mathbb{R} ⊂ \mathbb{C}
Безусловно теория множеств является более глубокой темой, но представленной теории тут достаточно для базового понимания последующих выражений и выводов.
Коротко о комплексных числах
Определение
Для определения необходимости комплексных чисел рассмотрим следующие преобразования квадратного уравнения:
x^2 + px + q = 0 ⇒ (x + p/2)^2 = p^2/4 - q ⇒ x + p/2 = ± \sqrt{p^2/4 - q} = ± \sqrt{D} ⇒ x = -p/2 ± \sqrt{D}
В школьной теории отрицательный дискриминант (D < 0) указывал на отсутствие корней, но если принять, что существует особое число i = \sqrt{-1} — мнимая единица, для которого i^2 = -1, то у данного уравнения появляются два решения:
x = -p/2 ± \sqrt{-|D|} = -p/2 ± i\sqrt{|D|}
В общем случае запись комплексных чисел имеет следующий вид:
z = a + bi, где a и b — действительные числа (\mathbb{R}), а i^2 = -1
Важное замечание: записи a + bi и a + ib эквивалентны между собой, так как мнимая единица обладает коммуникативностью с вещественными числами.
В таблице 1 представлены степени мнимой единицы:
| Степень | Значение |
|---|---|
| 0 | 1 |
| 1 | i |
| 2 | -1 |
| 3 | -i |
| 4 | 1 |
| 5 | i |
| 6 | -1 |
В таблице 1 можно заметить закономерность, которой будет уделено внимание позднее.
Множество, состоящее из элементов a + bi, для которого заданы операции сложения, вычитания, умножения и деления называется множеством комплексных чисел (\mathbb{C}), а каждый его элемент — комплексным числом.
Операции
Рассмотрим операции для данного множества.
Складывать и вычитать комплексные числа можно путем сложения и вычитания вещественных и мнимых частей:
(a_1 + b_1i) ± (a_2 + b_2i) = (a_1 ± a_2) + (b_1 ± b_2)i
Комплексное число можно умножать как на действительное, так и на другое комплексное число.
Произведение комплексного числа и действительного числа k:
k(a + bi) = ka + kbi
Произведение двух комплексных чисел:
(a_1 + b_1i) * (a_2 + b_2i) = a_1a_2 + a_1b_2i + b_1a_2i + b_1b_2i^2 = (a_1a_2 - b_1b_2) + (a_1b_2 + b_1a_2)i
Для выполнения деления двух комплексных чисел необходимо ввести понятие сопряженного числа:
z = (a + bi) \\
\overline{z} = (a - bi) \\
z\overline{z} = (a + bi) * (a - ib) = a^2 - abi + abi + b^2 = a^2 + b^2
Важное примечание: в некоторых источниках сопряженное комплексное число обозначается как z*
Деление двух комплексных чисел выполняется путем домножения числителя и знаменателя на сопряженное число знаменателя:
\frac{a_1 + b_1i} {a_2 + b_2i} = \frac{(a_1 + b_1i) * (a_2 - b_2i)} {(a_2 + b_2i) * (a_2 - b_2i)} = \frac{a_1a_2 - a_1b_2i + b_1a_2i - b_1b_2i^2} {a_2^2 + b_2^2} = \frac{a_1a_2 + b_1b_2} {a_2^2 + b_2^2} + \frac{b_1a_2 - a_1b_2} {a_2^2 + b_2^2}i
Комплексное число можно возвести в квадрат:
(a + bi)^2 = (a + bi) * (a + bi) = (a^2 - b^2) + 2abi
Сопряженное число так же может использоваться для получения абсолютного значения (величины) комплексного числа:
|z| = \sqrt{z\overline{z}} = \sqrt{a^2 + b^2}
Комплексная плоскость
Комплексной плоскостью называется плоскость, определенная двумя перпендикулярными осями: вещественной (горизонтально) и мнимой (вертикально). Пример такой плоскости изображен на рисунке 1.

На рисунке 1 можно увидеть наглядно закономерность из таблицы 1, определяющую поворот на 90°. Если взять любую точку, например p_1 = \frac{1}{2} + \frac{\sqrt{3}}{2}i, и умножить её на i, то точка повернется на угол, равный +90°:
p_2 = p_1 * i = (\frac{1}{2} + \frac{\sqrt{3}}{2}i) * i = \frac{1}{2}i + \frac{\sqrt{3}}{2}i^2 = -\frac{\sqrt{3}}{2} + \frac{1}{2}i
Аналогично поступим с точками p_3 = p_2 * i и p_4 = p_3 * i. Результаты поворота точек представлены на рисунке 2.

Выведем формулу для произвольного поворота точки.
Пусть величина числа p будет равна r: r = \sqrt{p\overline{p}} = \sqrt{a^2 + b^2}. Вынесем r за скобки: p = r(a/r + ib/r), причем (a/r)^2 + (b/r)^2 = 1.
Сумма квадратов синуса и косинуса угла φ равна единице: sin^2φ + cos^2φ = 1.
Тогда существует некоторый угол φ, такой что:
a/r = cosφ и b/r = sinφ,
благодаря чему можно получить тригонометрическую форму комплексных чисел:
p = r(cosφ + i*sinφ)
и их частную форму при радиусе r = 1:
p = cosφ + i*sinφ
Квадратное матричное уравнение
Рассмотрим уравнение следующего вида:
x^2 + Px + Q = O, где буквы P, Q и O являются квадратной матрицей второго порядка.
Важное замечание: прошу не путать заглавные буквы матриц с множествами, которые выделены жирным шрифтом.
Пусть существует единичная квадратная матрица Е:
E =
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}Тогда: P = p * E и Q = q * E — произведение действительных чисел p, q на единичную квадратную матрицу.
Примечание: любая степень E^n равна E.
Матрица O — нулевая матрица и она имеет следующий вид:
O =
\begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}Выделим полный квадрат из квадратного уравнения:
(x + P/2)^2 = P^2/4 - Q = E^2 * p^2/4 - E * q ⇒ x = E * -p/2 ± \sqrt{(p^2/4 - q) * E} = E * -p/2 ± \sqrt{D} * \sqrt{E}
Поскольку E^2 = \sqrt{E} = E, то решения такие же, как у уравнения с действительными числами.
Двойные числа
Существует матрица I, такая что I^2 = E, и она имеет следующий вид:
I =
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}Тогда выражение приобретает следующий вид:
x = E * -p/2 ± \sqrt{D} * I, при D > 0, если подставить матрицы:
x = -\frac{p}{2} *
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
+\sqrt{D} *
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}Можно выполнить перемножение и сложение и получить результат:
x =
\begin{pmatrix}
-\frac{p}{2} & \sqrt{D} \\
\sqrt{D} & -\frac{p}{2}
\end{pmatrix}
Так как единичная матрица E выполняет роль единицы, то её можно опустить в выражении и записать его в другом виде, называемом «алгебраическая запись двойных чисел»:
x = a + b * I
Двойными числами (иногда паракомплексными) называются гиперкомплексные числа вида a + b * I, где a и b — действительные, а I — квадратная матрица, такая что I^2 = 1. Если говорить проще, то двойными числами называется такое выражение, в котором присутствует единичная матрица и специальная матрица, такая что I^2 = 1
Важное замечание: иногда двойные числа называют дуальными и наоборот, но это не корректно, что будет раскрыто далее.
Двойные числа являются матрицами, но их можно умножать на число, складывать, вычитать и перемножать друг с другом. Далее приводятся формулы, получаемые аналогично с операциями над комплексными числами — раскрытием скобок и группировкой.
Сложение двух двойных чисел:
(a_1+I*b_1) ± (a_2+I*b_2) = (a_1 ± a_2) + I*(b_1 ± b_2)
Умножение:
(a_1+I*b_1) * (a_2+I*b_2) = (a_1a_2 + b_1b_2) + I*(a_1b_2 + a_2b_1)
Так же, как в случае с комплексными числами есть сопряжение и величина двойного числа, но с другим знаком:
|z| = \sqrt{z\overline{z}} = \sqrt{a^2 - b^2}
Примечание: автор не уходит глубже в теорию двойных чисел, так как для темы кватернионов более не требуется.
Дуальные числа
Вернемся к выражению при D = 0:
x = E * -p/2 ± \sqrt{0} * \sqrt{E} = E * -p/2 ± \sqrt{O}
Существует ненулевая матрица, квадрат которой равен нулю:
ε =
\begin{pmatrix}
0 & 1 \\
0 & 0
\end{pmatrix}При умножении такой матрицы на некое действительное число b получается следующий результат:
εb =
\begin{pmatrix}
0 & b \\
0 & 0
\end{pmatrix}Тогда выражение можно представить:
x = E * -p/2 ± εb = E * a ± εb = a ± εb, где E — единичная матрица, которую можно опустить.
Результат такой суммы будет иметь вид:
a+εb =
\begin{pmatrix}
a & b \\
0 & a
\end{pmatrix}Дуальными числами называют гиперкомплексные числа вида a + εb, где a и b — действительные числа, а ε — квадратная матрица, такая что ε^2 = 0.
Далее приводятся формулы, получаемые аналогично с операциями над комплексными числами — раскрытием скобок и группировкой.
Сложение дуальных чисел:
(a_1 + εb_1) + (a_2 + εb_2) = (a_1 + a_2) + ε(b_1 + b_2)
Умножение:
(a_1 + εb_1) + (a_2 + εb_2) = (a_1*a_2) + ε(a_1b_2 + a_2b_1)
Примечание: на примере умножения можно наглядно доказать ошибочность объединения терминов дуальных и двойных чисел.
Примечание: автор не уходит глубже в теорию дуальных чисел, так как для темы кватернионов более не требуется.
Комплексные числа как матрицы
Ранее в разделе определения комплексных чисел было выражение с отрицательным дискриминантом:
x = -p/2 ± \sqrt{-|D|} = -p/2 ± i\sqrt{|D|}, которое можно представить по-другому с помощью единичной матрицы:
x = -p/2 ± \sqrt{-|D|} = E * -p/2 ± \sqrt{|D|} * \sqrt{-E}
Из единичной матрицы, умноженной на минус единицу вполне возможно извлечь корень: i^2 = -E, где:
i =
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix}Важное замечание: можно использовать матрицу i = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} и как результат в разных источниках знак минус может перескакивать по побочной диагонали.
Тогда решением квадратного матричного уравнения будет матрица вида:
x = a*E + b*i = a*
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix} + b *
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix} =
\begin{pmatrix}
a & b \\
-b & a
\end{pmatrix}Вернемся к тригонометрической форме комплексных чисел для точки p:
p = r(cosφ + i*sinφ), изменим её с помощью квадратного матричного уравнения:
p = r *
\begin{pmatrix}
cosφ & sinφ \\
-sinφ & cosφ
\end{pmatrix}при умножении точки p (в обычной форме) на точку q (в тригонометрической форме) будет следующий результат:
p = a + ib \\
q = cosφ + i*sinφ \\
p*q = a' + ib' = (a + ib) * (cosφ + i*sinφ) ,
где штрихом обозначены изменившиеся координаты после поворота.
И в матричной форме:
\begin{pmatrix}
a' & b' \\
-b' & a'
\end{pmatrix} =
\begin{pmatrix}
cosφ & sinφ \\
-sinφ & cosφ
\end{pmatrix}
\begin{pmatrix}
a & b \\
-b & a
\end{pmatrix} Данное выражение является способом поворота против часовой стрелки произвольной точки на комплексной плоскости относительно начала координат.
Коротко о группах и телах
Группой называют непустое множество \mathbb{G} с определенной на нём бинарной операцией ∙.
Примечание: Здесь используется абстрактное множество \mathbb{G} с абстрактной операцией ∙, заместо которых в конкретном случае подставляется нужное множество или операция.
Группа требует соблюдение следующих аксиом:
- ассоциативность: для любых a, b и c из множества \mathbb{G} верно (a ∙ b) ∙ c = a ∙ (b ∙ c);
- наличие нейтрального элемента: в множестве \mathbb{G} существует элемент e такой, что для всех a из \mathbb{G} справедливо e ∙ a = a ∙ e = a;
- наличие обратного элемента: для любого a из множества \mathbb{G} найдется элемент a^{-1}, называемый обратным, такой, что a ∙ a^{-1} = a^{-1} ∙ a = e.
Важное замечание: в теории групп не обязательно свойство коммутативности для любых двух элементов a и b из множества \mathbb{G} : a ∙ b = b ∙ a, но если данное свойство выполняется, то группа называется коммутативной или абелевой.
Например: группа (\mathbb{Z}, +) — группа целых чисел с операцией сложения, где нейтральным элементом является 0 и данная группа является абелевой.
Группу можно представить как таблицу композиций результатов операции над парой элементов. Например: таблица сложения, умножения и т.д.
Поле — любое множество, где есть две операции сложения и умножения, связанные свойством дистрибутивности, и такие сложения это группа, а относительно умножения, за исключением нуля, это тоже группа.
Под дистрибутивностью понимается следующее свойство: a * (b + c) = a*b + a*c
Операция умножения кватернионов, рассматриваемая далее, не коммутативна. Для этого вводится понятие тело, которое обладает следующими свойствами:
- абелева группа относительно сложения;
- все ненулевые элементы образуют группу относительно умножения;
- дистрибутивность умножения относительно сложения.
Примечание: автор считает, что для дальнейшего понимания кватернионов общего понимания групп и тел достаточно.
Кватернионы
Определение
Термин кватерниона дан во введении.
Множество кватернионов обозначается: \mathbb{H}. Группа по сложению (\mathbb{H}, +) — коммутативна, а группа по умножению без нуля (\mathbb{H'}, *) не является коммутативной. При этом произведение кватерниона и вещественных чисел коммутативно.
Важное замечание: отсутствие коммутативности является весьма непривычной вещью в процессе изучения данной темы и требует повышенного внимания.
Если при переходе от вещественных к комплексным добавлялась одна мнимая компонента i: z = a + bi, то при переходе от комплексных к кватернионам необходимо добавить ещё одну компоненту j, которая не является частью комплексных чисел: q = (z_1 + z_2j), j ∉ \mathbb{C}.
Пусть z_1 и z_2 имеют следующий вид:
z_1 = a + bi,
z_2 = c + di,
тогда q = a + bi + (c + di)*j = a + bi + cj + d*(i*j). Определим произведение i*j = k, тогда итоговый вид кватерниона будет:
q = a + bi + cj + dk, где a — действительная часть, а bi + cj + dk — мнимая часть кватерниона.
Важное замечание: j — новый элемент, который не может быть равен i, дабы не получить в перемножении единицу.
Идея Гамильтона заключалась в следующем выражении:
i*j*k = -1.
Для определения знаков используется кольцо с поворотами по часовой или против часовой стрелки, представленное на рисунке 3.

По рисунку 3 можно сделать вывод, что если взять два элемента по часовой стрелке, то знак будет положительным и соответственно наоборот. Из чего следует, что порядок умножения важен и меняет знак, потому что группа по умножению не является коммутативной. На основании данного рисунка составим таблицу 2:
| i*j = k | j*i = -k |
| j*k = i | k*j = -i |
| k*i = j | i*k = -j |
Квадраты всех компонент равны отрицательной единице:
i^2 = j^2 = k^2 = -1
При умножении любой компоненты на -1 у неё меняется знак.
Гамильтон заметил, что мнимые компоненты можно использовать для представления трех декартовых единичных векторов i, j, k. Данное использование представлено на рисунке 4.
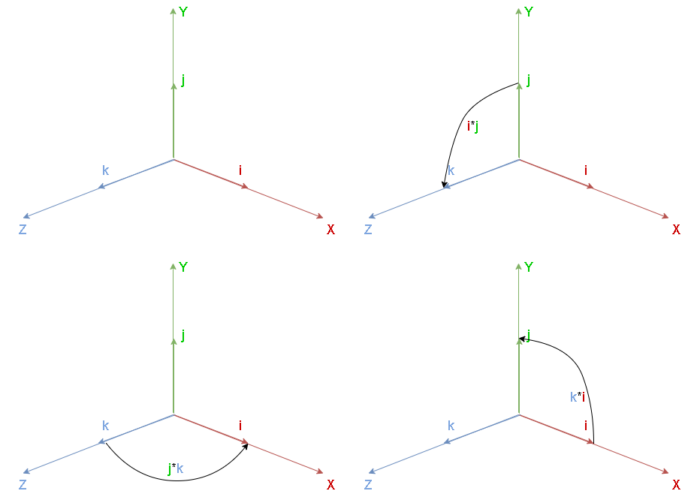
Так же по рисунку 4 можно увидеть графическое представление поворота против часовой оси с рисунка 3.
Можно заменить b, c и d на x, y, z для соответствия рисунку:
q = a + xi + yj + zk.
Для удобства записи в некоторых операциях представим кватернион как упорядоченную пару:
q = [a, v], где a = S(q) — действительная часть, а v = V(q) = bi+cj+dk — мнимая часть кватерниона, которая так же может быть представлена: v = V(q) = xi+yj+zk. Под функциями S(q) и V(q) следует понимать отделение соответствующих частей кватерниона: действительной и мнимой.
Геометрический оператор
Кватернион как геометрический оператор можно описать через отношение двух векторов:
\frac{\overrightarrow{b}}{\overrightarrow{a}} = q или \overrightarrow{b} = q\overrightarrow{a}. Данная связь продемонстрирована на рисунке 5.

При преобразовании вектора \overrightarrow{a} к вектору \overrightarrow{b} производится две операции:
- тензор — изменение длинны вектора \overrightarrow{a} в соответствие длине вектора \overrightarrow{b};
- версор — поворот вектора \overrightarrow{a} в направлении вектора \overrightarrow{b}.
Кватернион можно определить через эти операции: q = Tensor(q)Versor(q)
Выразим векторы \overrightarrow{a} и \overrightarrow{b} через единичные:
\overrightarrow{a} = \overrightarrow{OA} = A\hat{a}\\
\overrightarrow{a} = \overrightarrow{OB} = B\hat{b}\\
\overrightarrow{c} = \overrightarrow{CB} = Bsinφ*\hat{c}. Эти векторы изображены на рисунке 6.
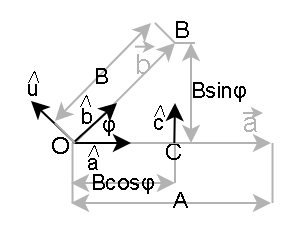
По рисунку 6 можно определить: q = \frac{\overrightarrow{a}}{q\overrightarrow{b}} = \frac{B\hat{b}}{A\hat{a}}
Отрезок BC на котором лежит \hat{c} перпендикулярен вектору \overrightarrow{a}. Определим:
\overrightarrow{OC} = Bcosφ*\hat{a}\\
\overrightarrow{CB} = Bsinφ*\hat{c}\\
\overrightarrow{OB} = \overrightarrow{OC} + \overrightarrow{CB}\\
\frac{\overrightarrow{OB}}{\overrightarrow{OA}} = \frac{\overrightarrow{OC}+\overrightarrow{CB}}{\overrightarrow{OA}}=\frac{\overrightarrow{OC}}{\overrightarrow{OA}} + \frac{\overrightarrow{CB}}{\overrightarrow{OA}}\\
\frac{\overrightarrow{b}}{\overrightarrow{a}} = \frac{Bcosφ*\hat{a}}{A\hat{a}} + \frac{Bsinφ*\hat{c}}{A\hat{a}}\\
q = \frac{B}{A}cosφ + \frac{B}{A}sinφ*\frac{\hat{c}}{\hat{a}} = \frac{B}{A}(cosφ + sinφ*\frac{\hat{c}}{\hat{a}})
Пусть частное двух векторов \hat{c} и \hat{a} будет равно \hat{u}:
\hat{u} = \frac{\hat{c}}{\hat{a}},
тогда кватернион будет иметь итоговый вид:
q = \frac{\overrightarrow{b}}{\overrightarrow{a}} = \frac{B}{A}(cosφ + \hat{u}sinφ)
Из этого выражения можно отметить тензор: Tensor(q) = \frac{B}{A}, и версор: Versor(q) = cosφ + \hat{u}sinφ.
Для записи через упорядоченную пару потребуется перемножить тензор и версор:
S(q) = \frac{B}{A}cosφ\\
V(q) = \frac{B}{A}\hat{u}sinφ\\
q = S(q) + V(q) = [\frac{B}{A}cosφ, \frac{B}{A}\hat{u}sinφ]
Операции
Кватернионы складываются и вычитаются аналогично комплексным числам:
q_1 = [a_1, v_1], \\
q_2 = [a_2, v_2], \\
q_1 ± q_2 = [a_1 ± a_2, v_1 ± v_2] = (a_1 ± a_2) + (b_1 ± b_2)i + (c_1 ± c_2)j + (d_1 ± d_2)k
Произведение кватернионов:
q_1 * q_2 = [a_1, v_1] * [a_2, v_2] = (a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2) + (a_1b_2 + a_2b_1 + c_1d_2 - d_1d_2)i + (a_1c_2 + a_2c_1 + d_1b_2 - d_2b_1)j + (a_1d_2 + a_2d_1 + b_1c_2 - b_2c_1)k
Но данную формулу нельзя назвать очень удобной для человека, попробуем её упростить. Для этого потребуется ввести сопряжение для кватернионов.
Кватернионы имеют свое сопряжение:
q = [a, v], \\
\overline{q} = [a, -v] = a - bi - cj - dk,
или в другой форме:
q = w_1 + w_2j, \\
\overline{q} = \overline{w_1 + w_2j} = \overline{w_1} - w_2j
Основное свойство кватернионов связано с их сопряжением:
\overline{q_1*q_2} = \overline{q_2} * \overline{q_1}, следовательно для любых двух из (1,i,j,k) и (1,i,j,k) применимо следующее правило:
\overline{ik} = \overline{-j} = j \\
\overline{ik} = \overline{k}*\overline{j} = -k * -i = ki = j
Следствие: для любого q выражение q\overline{q} является действительным (\mathbb{R}). Это можно доказать подтвердив следующее предположение: если число равно своему сопряжению, которое меняет знаки у мнимой части, то оно вещественное.
В выражении j*z, где z — комплексное число, можно поменять множители местами, заменив комплексное его сопряженным:
j*z = j * (a+bi) = aj - bk = (a+bi)j = \overline{z}j, где произведение j*i = -k
Представим произведение кватернионов в следующем виде:
q_1 = (z_1 + z_2j), \\
q_2 = (w_1 + w_2j), где z_1, z_2, w_1, w_2 — комплексные числа, тогда:
q_1*q_2 = (z_1 + z_2j)(w_1 + w_2j) = z_1w_1 + z_2jw_1 + z_1w_2j + z_2jw_2j = z_1w_1 + z_2\overline{w_1}j + z_1w_2j + z_2\overline{w_2}j^2 = (z_1w_1 - z_2\overline{w_2}) + (z_2\overline{w_1} + z_1w_2)j — такая форма является более понятной для человека.
Вернемся к «неудобной» записи произведения и сгруппируем её по-другому для упорядоченной пары:
q_1 * q_2 = [a_1, v_1] * [a_2, v_2] = (a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2) + i(c_1d_2 - c_2d_1) + j(b_2d_1 - b_1d_2) + k(b_1c_2 - b_2c_1) + a_1(b_2i+c_2j+d_2k) + a_2(b_1i+c_1j+d_1k) = [a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2, v_1⨯ v_2 + a_1v_2 + a_2v_1], где v_1⨯ v_2 — векторное произведение, равное:
v_1⨯ v_2 = i(c_1d_2 - c_2d_1) + j(b_2d_1 - b_1d_2) + k(b_1c_2 - b_2c_1),
или с координатами осей:
[a_1a_2 - x_1x_2 - y_1y_2 - z_1z_2, v_1⨯ v_2 + a_1v_2 + a_2v_1], где v_1⨯ v_2 — векторное произведение, равное:
v_1⨯ v_2 = i(y_1z_2 - y_2z_1) + j(x_2z_1 - x_1z_2) + k(x_1y_2 - x_2y_1)
Норма кватерниона:
N(q) = q\overline{q}
Норма произведения двух кватернионов равна произведению их норм:
N(q_1 * q_2) = N(q_1) * N(q_2)
Д-во: N(q_1) * N(q_2) = q_1q_2\overline{q_2}\overline{q_1}, так как q_2\overline{q_2} = N(q_2)∈\mathbb(R) = (*_1), а вещественные коммутируют с кватернионами: (*_1) = N(q_2) * q_1\overline{q_1} = N(q_1)N(q_2)
Выполним умножение кватерниона с его сопряженным:
(a+bi+cj+dk)(a-bi-cj-dk) = a^2 + b^2 + c^2 + d^2, что по сути является четырехмерной сферой.
Модуль кватерниона (его абсолютное значение или величина):
|q| = \sqrt{q\overline{q}} = \sqrt{a^2+b^2+c^2+d^2}
Расстояние между двумя кватернионами равно:
ρ(q_1, q_2) = |q_1 - q_2| = \sqrt{(a_1-a_2)^2+(b_1-b_2)^2+(c_1-c_2)^2+(d_1-d_2)^2}
Деление кватернионов: для каждого ненулевого кватерниона определено заведомо положительное вещественное число, равное произведению его на сопряжение (норма):
q^{-1} = \frac{\overline{q}}{N(q)},
что можно проверить следующим выражением:
q*q^{-1} = q*\frac{\overline{q}}{N(q)} = \frac{q\overline{q}}{N(q)} = 1, исходя из определения нормы.
Важное замечание: qx_1 = w и x_2q = w — разные выражения. Чтобы это доказать умножим обе части на q^{-1}.
Левое:
q^{-1}qx_1 = q^{-1}w \\
x_1 = q^{-1}w,
Правое:
x_2qq^{-1} = wq^{-1} \\
x_2 = wq^{-1}, а кватернионы с комплексными не коммутируют.
Скалярное произведение:
rq = [r,0][a,v] = r(a + bi + cj + dk) = ra + r(bi + cj + dk) = [ra,rv] = qr,
или с координатами осей:
rq = [r,0][a,v] = r(a + xi + yj + zk) = ra + r(xi + yj + zk) = [ra,rv] = qr,
Вращение
В случае с вращением, задаваемым комплексными числами на двумерной плоскости, модуль комплексного числа не изменяется.
В случае с кватернионами модуль мнимой части изменяется. Пусть даны два кватерниона, такие что:
q_1 = i + j + k, |q_1| = \sqrt{3}, |V(q_1)| = \sqrt{3} \\
q_2 = i, |q_2| = \sqrt{1} = 1, |V(q_2)| = 1,
тогда результат их произведения:
q_2 * q_1 = i(i + j + k) = ii + ji + ki = -1 + k - j, V(q_1 * q_2) = +k - j, его длина равна:
|q_1 * q_2| = \sqrt{3}, |V(q_1 * q_2)| = \sqrt{2} ⇒ |q_1 * q_2| ≠ |V(q_1 * q_2)|.
Таким образом, требуется специальное умножение для трехмерных вращений:
Ψ_q = q_2 * q_1 * q_2^{-1}
Определим длину результата по описанной формуле Ψ_q:
Ψ_q = i * (i + j + k) * \frac{\overline{i}}{N(i)} = i * (i + j + k) * \overline{i} = (*_2) , так как N(i) = 1, а \overline{i} = -i, то (*_2) = i * (i + j + k) * (-i) = (ii + ij + ik) * (-i) = (-1 + k - j) * (-i) = i - ki + ji = i - j - k, |q_2q_1q_2^{-1}| = \sqrt{3} \\
V(q_2q_1q_2^{-1}) = i - j - k, |V(q_2q_1q_2^{-1})| = \sqrt{3}\\
|q_1| = |q_2q_1q_2^{-1}|, |V(q_1)| = |V(q_2q_1q_2^{-1})|, как видно из вычислений — длины совпадают.
Важное замечание: иногда данную формулу поворота можно встретить в следующей форме: Ψ_q = pqp* = pqp^{-1}
Поворот Ψ_q может быть записан в матричной форме:
Ψ_q = q_2q_1q_2^{-1} =
\begin{pmatrix}
a_2^2 + x_2^2 - y_2^2 - z_2^2 & 2x_2y_2-2a_2z_2 & 2x_2z_2+2a_2y_2 \\
2x_2y_2 + 2a_2z_2 & a_2^2 - x_2^2 + y_2^2 - z_2^2 & 2y_2z_2 - 2a_2x_2\\
2x_2z_2 - 2a_2y_2 & 2y_2z_2 +2a_2x_2 & a_2^2 - x_2^2 - y_2^2 + z_2^2
\end{pmatrix}
\begin{pmatrix}
q_1.x\\
q_1.y\\
q_1.z
\end{pmatrix},где q_1 = [0, v_1], q_2 = [a_2, v_2].
В частном случае, когда q_1 имеет длину равную единице:
Ψ_q = q_2q_1q_2^{-1} =
\begin{pmatrix}
1 - y_2^2 - z_2^2 & 2x_2y_2-2a_2z_2 & 2x_2z_2+2a_2y_2 \\
2x_2y_2 + 2a_2z_2 & 1 + y_2^2 - z_2^2 & 2y_2z_2 - 2a_2x_2\\
2x_2z_2 - 2a_2y_2 & 2y_2z_2 +2a_2x_2 & 1 - y_2^2 + z_2^2
\end{pmatrix}
\begin{pmatrix}
q_1.x\\
q_1.y\\
q_1.z
\end{pmatrix},Примечание: если требуется матрица 4х4, то необходимо добавить строку и столбец нулей, оставив последний диагональный элемент равным единице.